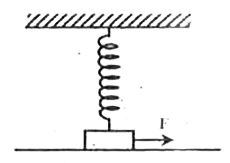
A block placed on a smooth horizontal floor is connected to a springs as shown. Initially an external force of 100N keeps it stretched by 1cm beyond natural lenjgth i equilibrium. This force is now removed and another force F is applied on this block, which slowly moves it from this position to a position where the spring is finally compressed by 3cm. Find the work done by this force F (in joules).

The correct Answer is:4
Force constant k=1000.1104Nm
W=12k(x2final−x2initial)=4J
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A spring is attached with a block of mass m and a fixed horizontal roof as shown. The block is lying on a smooth horizontal table and initially the spring is vertical and unstretched. Natural length of spring is 3l0. A constant horizontal force F is applied on the block so that block moves in the direction of force. When length of the spring becomes 5l0, block leaves contact with the table. Find the constant force F, if initial and final velocity of block is zero.
View SolutionA spring is attached with a block of mass m and a fixed horizontal roof as shown. The block is lying on a smooth horizontal table and initially the spring is vertical and unstretched. Natural length of spring is 3l0. A constant horizontal force F is applied on the block so that block moves in the direction of force. When length of the spring becomes 5l0, block leaves contact with the table. Find the constant force F, if initial and final velocity of block is zero.

View Solution
Knowledge Check
When a force of 0.1 N is applied, the spring is stretched by 1.5 cm. The spring is cut into three parts and one part is stretched by 3 cm. Find the force required for doing so.
A0.2 NB0.3 NC0.4 ND0.6 NWhen a force of 0.1 N is applied, the spring is stretched by 1.5 cm. The spring is cut into three parts and one part is stretched by 3 cm. Find the force required for doing so.
A0.2 NB0.3 NC0.4 ND0.6 NA block attached to a spring, pulled by a constant horizontal force, is kept on a smooth surface as shown in figure. Initially, the spring is in the natural length state. Then the maximum positive work that the applied force F can do is (give that string does not break)
 A(a) F2kB(b) 2F2kC(c) ∞D(d) F22k
A(a) F2kB(b) 2F2kC(c) ∞D(d) F22k
A block attached to a spring, pulled by a constant horizontal force, is kept on a smooth surface as shown in figure. Initially, the spring is in the natural length state. Then the maximum positive work that the applied force F can do is (give that string does not break)

View SolutionA block attached to a spring, pulled by a constant horizontal force, is kept on a smooth surface as shown in figure. Initially, the spring is in the natural length state. Then the maximum positive work that the applied force F can do is (give that string does not break)

View SolutionA spring block system is placed on a rough horizontal floor. Force constant of the spring is k. The block is pulled to right to give the spring an elongation equal to x0 and then it is released. The block moves to left and stops at the position where the spring is relaxed. Calculate the maximum kinetic energy of the block during its motion.
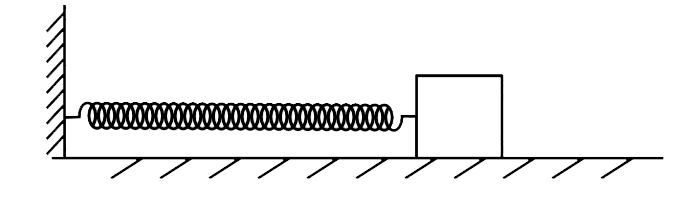
View SolutionA block of mass m=2kg is connected to a spring of force constant k=50n/m. Initially the block is at rest and the spring has natural length . A constant force f=60N, is applied horizontally towards right, the maximum speed of the block (in m/s will be (neglect frication).

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
