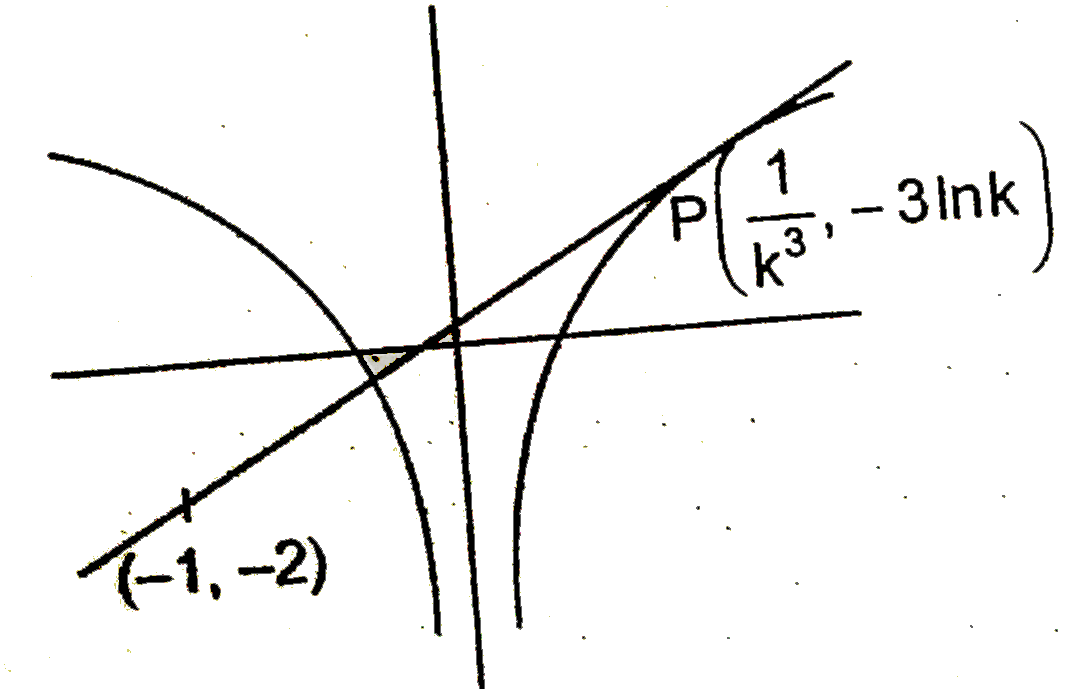
If f(x)=k3x+k3−2 cuts the curve g(x)=12Inx2 at exactly one point 'k' may lie in the interval
(1√e,e)
(1e,1√e)
(1e2,1e)
none of these
The correct Answer is:A
−3Ink+21k3+1=k3
So, f(x)=k3+3Ink−1
f(1√e)f(e)<0
Topper's Solved these Questions
Similar Questions
Let f(x)=x3−3x2+2x . If the equation f(x)=k has exactly one positive and one negative solution then the value of k equals. −2√39 (b) −29 23√3 (d) 13√3
View SolutionIf the equation sin4x−(k+2)sin2x=(k+3) has a solution then 'k' must lie in the interval: a.(−4,−2) b. [−3,2) c. (−4,−3) d. [−3,−2]
View Solution
Knowledge Check

If g(x)=−2 intersects the graph of y=f(x)+k at one point, which of these choices could be the value of k?A−1.5B−0.5C0D1.5The value of k for which the equation 3x2+2x(k2+1)+k2−3k+2=0 has roots of opposite signs, lies in the interval
A(−∞,0)B(−∞,−1)C(1,2)D(3/2,2)
If the equation x2−(2k+1)x+(3k+2)=0 has exactly one root in (-1, 4), then the possible interval of the values of k is
View SolutionIf the equation sin4x−(k+2)sin2x=(k+3) has a solution then 'k' must lie in the interval: a.(−4,−2) b. [−3,2) c. (−4,−3) d. [−3,−2]
View SolutionShow that the curves 2x=y2 and 2xy=k cut at right angles, if k2=8 .
View SolutionShow that the curves 2x=y2 and 2xy=k cut at right angles, if k2=8 .
View SolutionThe value of k for which the equation 3x2+2x(k2+1)+k2−3k+2=0 has roots of opposite signs, lies in the interval
View SolutionThe set of values of k for which roots of the equation x2−3x+k=0 lie in the interval (0, 2), is
View Solution
