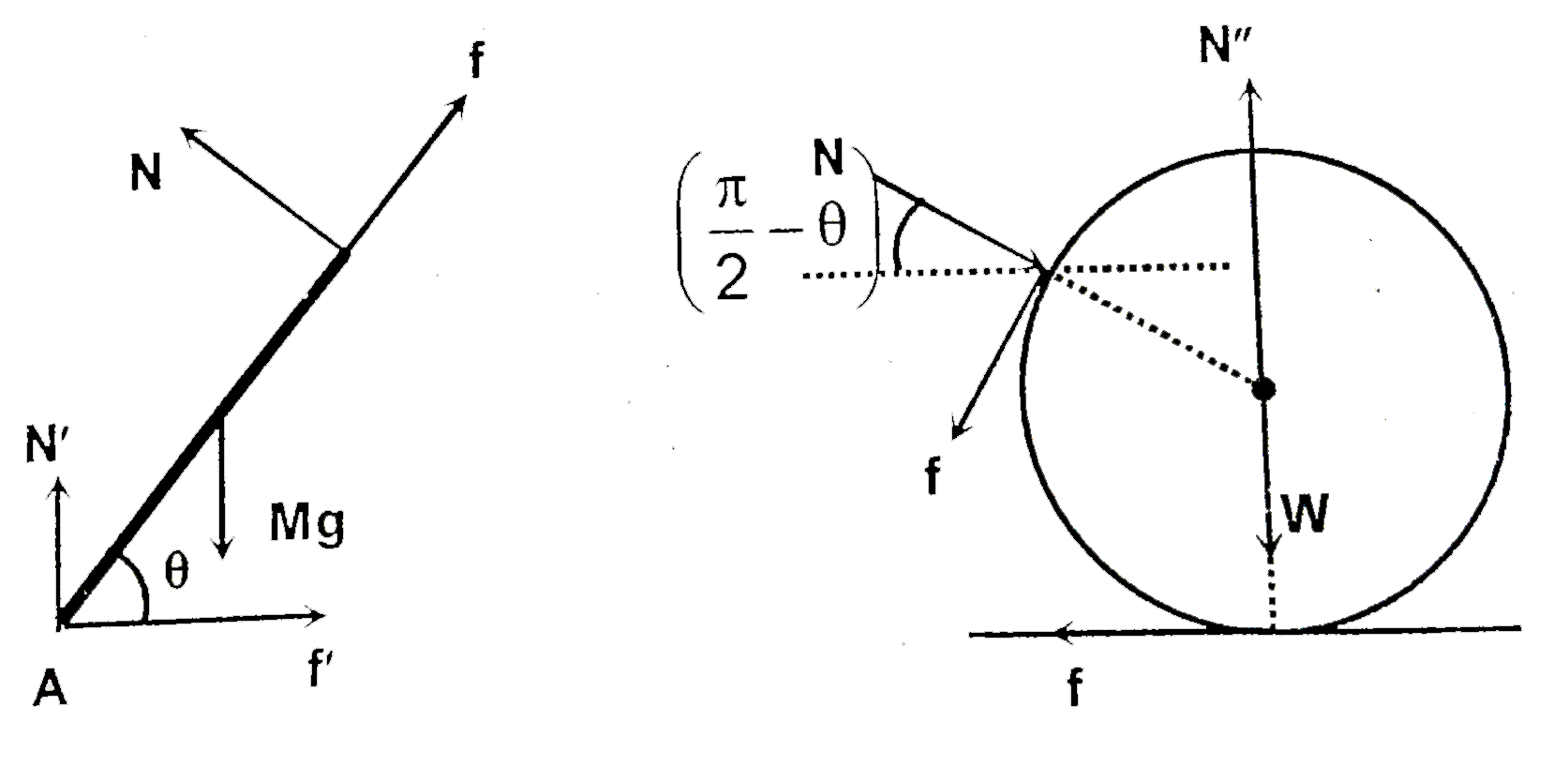
A stick o fmas density λ=8kg/m rests on a disc of radius R=20cm as shown in the figure. The stick makes an angle θ=37∘ with the horizontal and is tangent to the disc at its upper end. Friction exists at all point of contact and assume that it is large enough to keep the system at rest. Find the friction force (in Newton) between the ground and the disc. (take g=10m/s2)

The correct Answer is:00006.40
τA=0
N=Mg2cosθ
For disc, Nsinθ=f+fcosθ
∴f=Nsinθ1+cosθ=Mgsinθcosθ2(1+cosθ)
M=λL and L=rtanθ2
f=12λRcosθ
=12×8×10×210×45
=325=6.40N
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A coin placed on a horizontal rotating disc, with its centre at 10 cm from the centre of the disc, is about to slip off when the disc performs 60 rpm. Find the coefficient of friction between the coin and the disc.
View SolutionTwo forces of magnitude F are acting on a uniform disc kept on a horizontal rough surface as shown in the figure. Friction force by the horizontal surface on the disc is nF. Find the value of n.

View Solution
Knowledge Check
A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
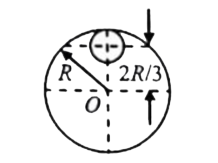 A4MR2B9MR2C379MR2D409MR2
A4MR2B9MR2C379MR2D409MR2From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
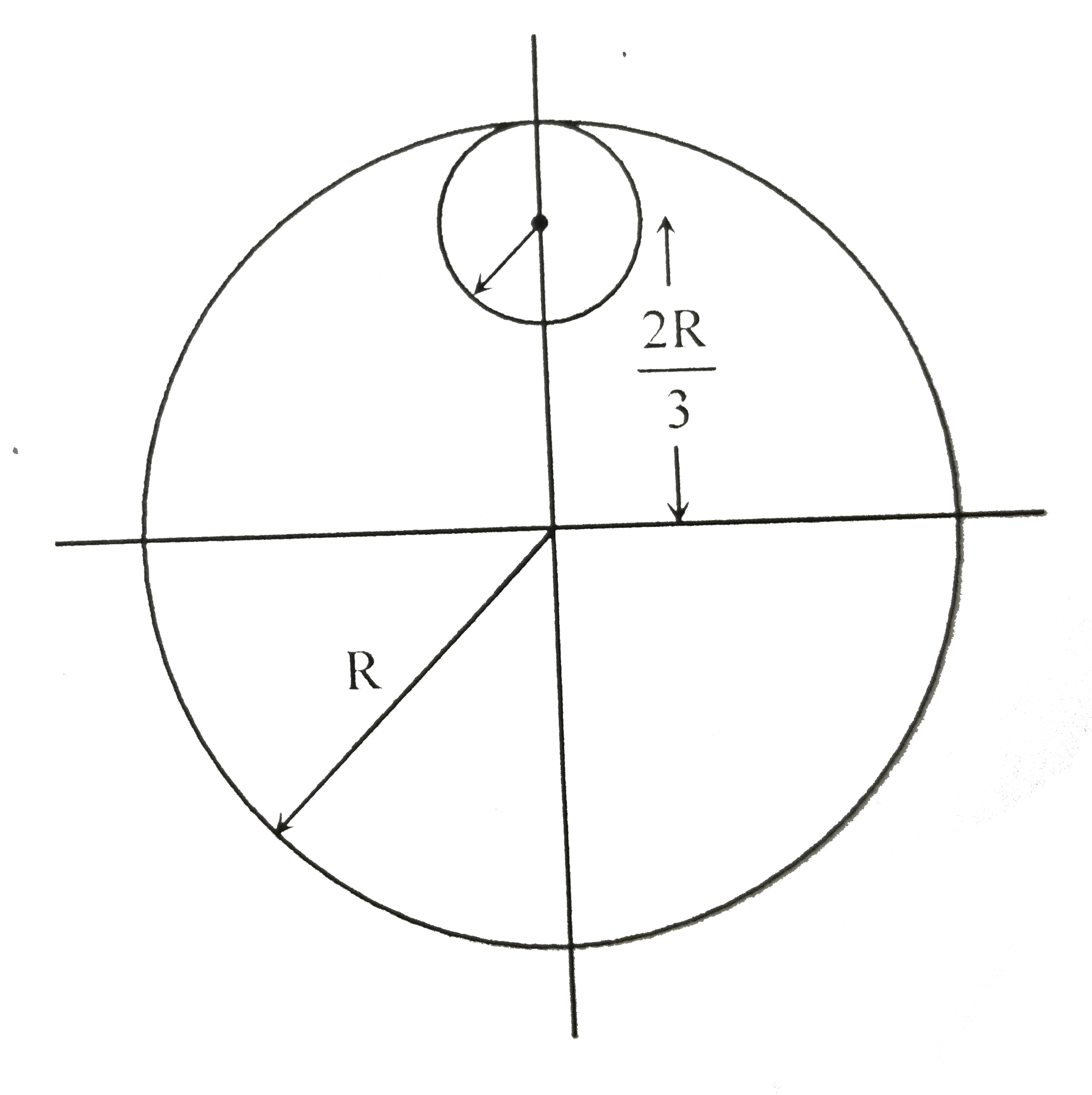 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
Two forces of magnitude F are acting on a uniform disc kept on a horizontal rough surface as shown in the figure. Friction force by the horizontal surface on the disc is nF. Find the value of n.

View SolutionA uniform disc of mass m and radius R is rolling up a rough inclined plane which makes an angle of 30∘ with the horizontal. If the coefficients of static and kinetic friction are each equal to μ and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane.
View SolutionA uniform disc of mass m and radius R is rolling up a rough inclined plane which makes an angle of 30∘ with the horizontal. If the coefficients of static and kinetic friction are each equal to μ and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane.
View SolutionA uniform disc of radius R=20cm has a round cut as shown in figure. The mass of the remaining (shaded) portion of the disc equals m=7.3kg. Find the moment of inertia of such a disc relative to the axis passing through its centre of inertia and perpendicular to the plane of the disc.

View SolutionA gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:

friction between the grasscutter (assumed as a disc) and ground.
View Solution
