A solid cube is floating (completely submerged) in a container filled with some liquid. The system is heated slowly. Ramesh states that cube will slowly sink. Suresh immediately responds that on the contary it will rise. Choose CORRECT statement(s)
Ramesh is right
Suresh is right
Without the knowledge of the thermal expansion coefficient of the cube and fluid, the question can not be decided clearly
One of them may be correct
The correct Answer is:C, D
If the cube has a coefficient of thermal expension greater than liquid then buoyancy force will dominate
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A beaker contains a liquid of volume V0. A solid block of volume V floats in the liquid with 90% of its volume submerged in the liquid. The whole system is heated to raise its temperature by Δθ. It is observed that the height of liquid in the beaker does not change and the solid in now floating with its entire volume submerged. Calculate Δθ. It is given that coefficient of volume expansion of the solid and the glass (beaker) are γs and γg respectively.
View SolutionJini took a container completely filled with some ice cubes floating on it. He observed the container expecting that water to overflow after the ice melted. Can you predict what he would finally see?
View Solution
Knowledge Check
Figure shows a container filled with a liquid of density ρ. Four points A,B,C and D lie on the vertices of a vertical square. Points A and C lie on a vertical line and points B and D lies on a horizontal line. Choose the correct statement(s) about the pressure at the four points.
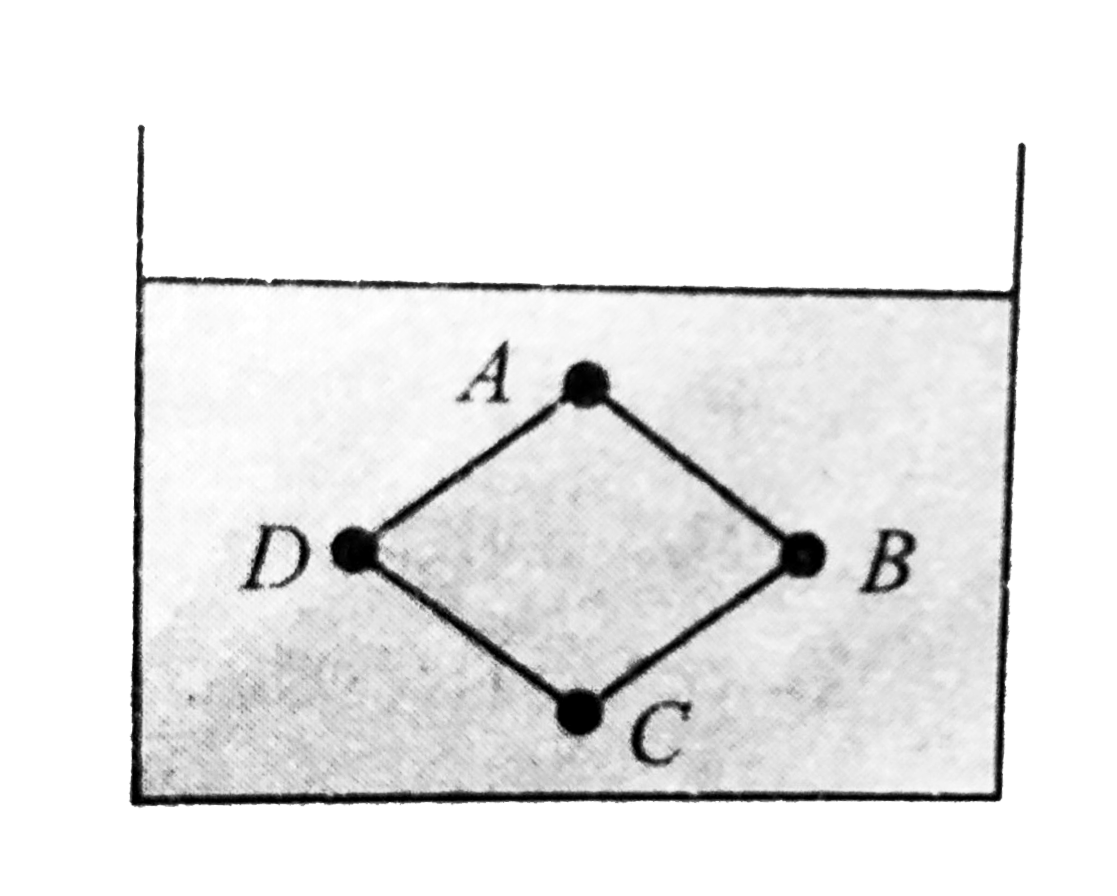APD=PBBPA<PB=PD<PCCPD=PB=PC−PA2DPD=PB=PC+PA2A solid cube floats in a liquid of density ρ with half of its volume submerged as shown. The side length of the cube is a, which is very small compared to the size of the container. Now a liquid of density ρ3 (immiscible with the liquid already in the container) is poured slowly into the container. The column of the liquid of density ρ3 that must be poured so that the cube is fully submerged (with its top surface coincident with the surface of the poured liquid) is :
Aa3Ba2C2a3D3a4A small solid ball of density ρ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density 4ρ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)
AFor ball to hit the top of container at end Q,a=3gBFor ball to hit the top of container at end Q,a=2gCBall hits the top of container at end Q after a time t=√L3gDBall hits the top of container at end Q after a time t=√2L3g
Jini took a container completely filled with some ice cubes floating on it. He observed the container expecting that water to overflow after the ice melted. Can you predict what he would finally see?
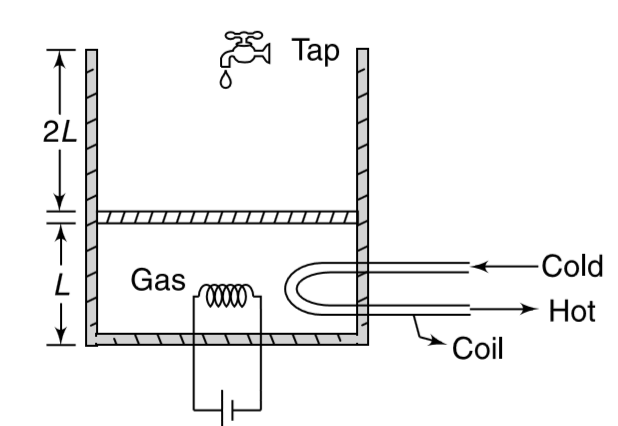
View SolutionA cylindrical container of height 3L and cross sectional area A is fitted with a smooth movable piston of negligible weight. It contains an ideal diatomic gas. Under normal atmospheric pressure P0 the piston stays in equilibrium at a height L above the base of the container. The gas chamber is provided with a heater and a copper coil through which a cold liquid can be circulated to extract heat from the gas. Volume occupied by the heater and the liquid coil is negligible. Following set of operations are performed to take the gas through a cyclic process.
(1) Heater is switched on. At the same time a tap above the cylinder is opened. Water fills slowly in the container above the piston and it is observed that the piston does not move. Water is allowed to fill the container so that the height of water column becomes L. Now the tap is closed.
(2) The heater is kept on and the piston slowly moves up. Heater is switched off at the time water is at brink of overflowing.
(3) Now the cold liquid is allowed to pass through the coil. The liquid extracts heat from the gas. Water is removed from the container so as to keep the position of piston fixed. Entire water is removed and the gas is brought back to atmospheric pressure.
(4) The circulation of cold liquid is continued and the piston slowly falls down to the original height L above the base of the container. Circulation of liquid is stopped. Assume that the container is made of adiabatic wall and density of water is ρ. Force on piston due to impact of falling water may be neglected.
(a) Draw the entire cycle on a P–V graph.
(b) Find the amount of heat supplied by the heater and the amount of heat extracted by the cold liquid from the gas during the complete cycle.
View SolutionA capacitor of capacity C0 is conneted to a battery of emfV0 When steady state is attained a dielectric slab of dielectric constant K is slowly introduced in the capacitor to fill the capacitor completely. Mark the correct statement(s), in final stady state.
View SolutionThe system shown in the figure is in equilibrium. The piston is massless, frictionless and insulated. All walls of the chamber are also insulated. When heat is generated inside the lower chamber the piston slowly moves upwards by 2 m and the liquid comes out through an orifice so that it can rise to a maximum height of 5 m above the orifece level. The lower chamber contains 2 moles of an ideal monoatomic gas at 500k .
Area of orifice a =0.05m2
Area of the piston A=1m2
Density of the liquid, ρ=103kg/m3 , g=10m/s2
Atmospheric pressure, Patm=105N/m2
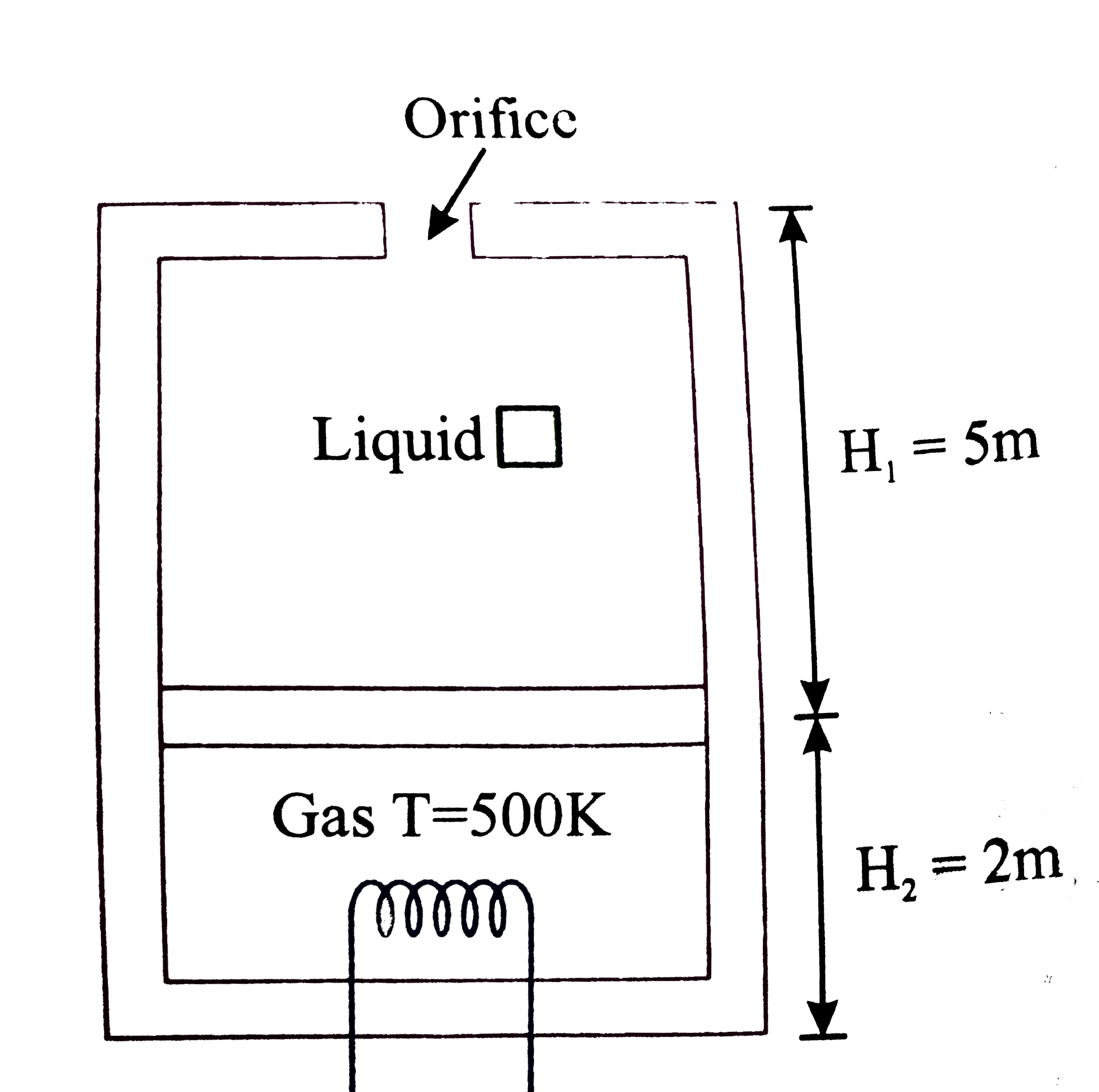
The final pressure of the gas is
View SolutionThe system shown in the figure is in equilibrium. The piston is massless, frictionless and insulated. All walls of the chamber are also insulated. When heat is generated inside the lower chamber the piston slowly moves upwards by 2 m and the liquid comes out through an orifice so that it can rise to a maximum height of 5 m above the orifece level. The lower chamber contains 2 moles of an ideal monoatomic gas at 500k .
Area of orifice a =0.05m2
Area of the piston A=1m2
Density of the liquid, ρ=103kg/m3 , g=10m/s2
Atmospheric pressure, Patm=105N/m2
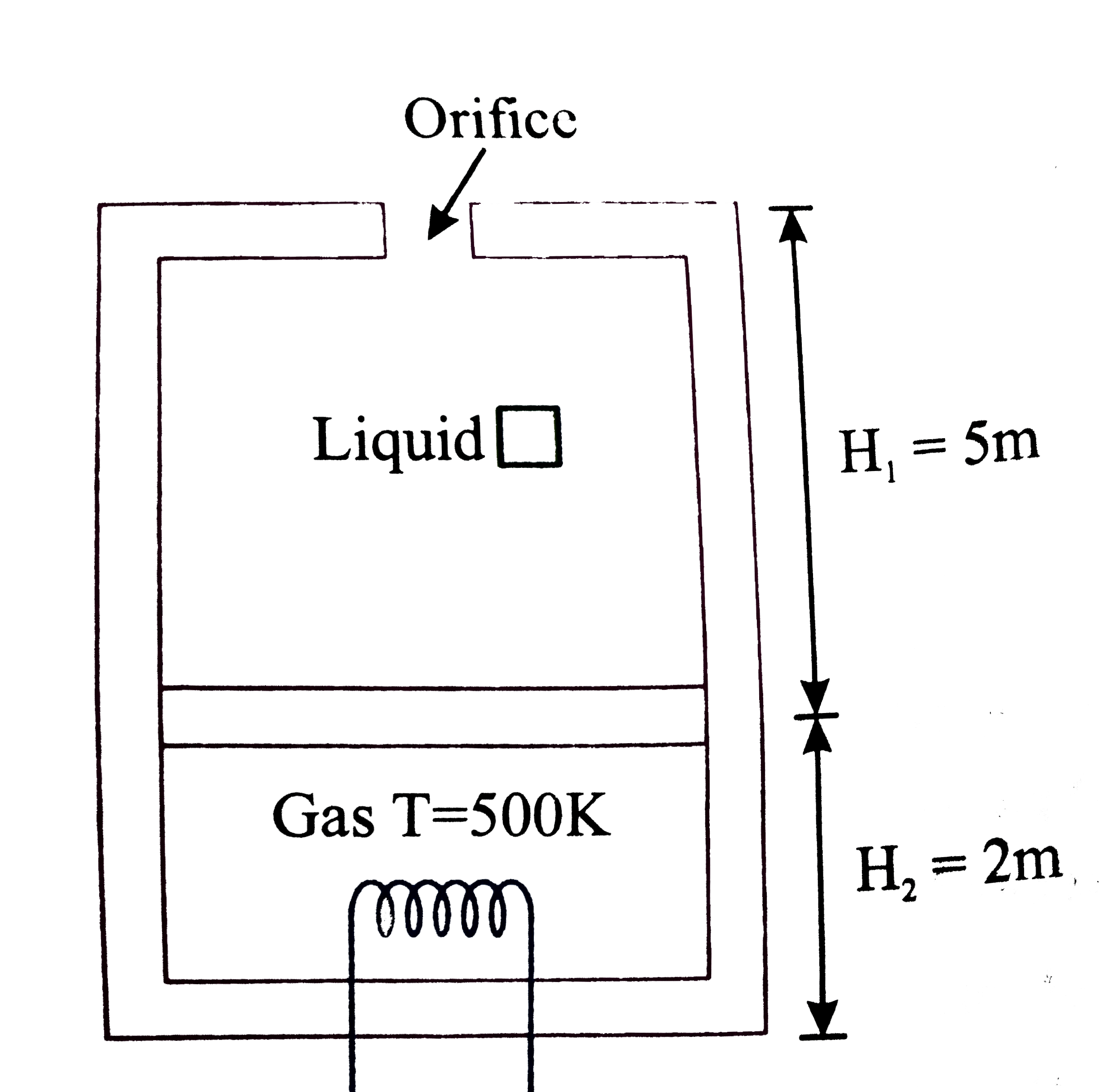
The average power of the heater is
View Solution