A regular tetrahedron frame is made up of homogeneous resitance wire of uniform cross section. Current I enters vertex A through a long, straight wire directed towards the centre O of the tetrahedron and is conducted away through vertex B in the same way, as illustrated in the figure. Choose CORRECT statement (s)

There is no current through wire DC because point D cand C are equipotential
Current through wire AB is
Current through wire AC is
Net magnetic field at point O is zero
The correct Answer is:A, B, C, D
From symmetry
and and net field at centre is zero
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic48videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics15videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS45videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
A direct current I=10A a flows in a long straight round conductor. Find the magnetic flux through a half of wire's cross-section per one meter of its length.
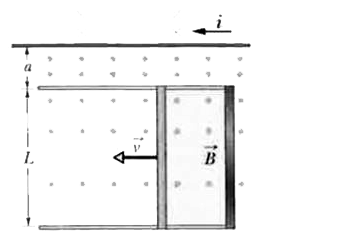
View SolutionFigure 30-50 shows a rod of length L = 12.0 cm that is forced to move at constant speed v = 5.00 m/s along horizontal rails. The rod, rails, and connecting strip at the right form a conducting loop. The rod has resistance 0.400 Ω the rest of the loop has negligible resistance. A current i = 100 A through the long straight wire at distance a= 5.00 mm from the loop sets up a (nonuniform) magnetic field through the loop. Find the (a) emf and (b) current induced in the loop. (c) At what rate is thermal energy generated in the rod? (d) What is the magnitude of the force that must be applied to the rod to make it move at constant speed? (e) At what rate does this force do work on the rod?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A long straight wire of negligible resistance is bent into V shape, its two arms making an angle α with each other and placed horizotally in a vertical, homogeneous field B. A rod of total mass m, and resistance r per unit length, is placed on V shaped conductor, at a distance x0 from its vertex A, and perpendicular to the bisector of angle α (see fegure)

The rod is started off with an initial veloctiy v0 in the direction of bisector and away from vertex A. The rod is long enough not to fall off the wire during the subsquent motion, and the electrical contact between the two is good although friction between them is negligible. Choose CORRECT statements(s)AAt any position x, let velocity of wire is v thenB2rx20tan,α2+mV0=B2rx2tan,α2+mvBmaximum value of x cordinate of wire is xmax=√x20+mv0rB2tan,α2CAs x increases, v decreaseDWhatever is the direction of vertical magnetic field, the rod will ultimately stop, - Question 2 - Select One
Electric current i enters and leaves a square loop made of homogeneous wire of uniform cross-section through diagonally opposite corners.A charge particle q moving along the axis of the square loop.Passes through centre at speed v.The magnetic force acting on the particle when it passes through the centre has a magnitude
Aqvμ0i2aBqvμ0i2πaCqvμ0iaDzero - Question 3 - Select One
If a square frame of side L is made from a uniform wire and current I is flowing through it and its magnetic field intensity at the centre is B1. When the same current is passed through the circular loop whose circumference is same as that of the square, the magnetic field at the centre is B2. What will be B1/B2 ?
A4√2π3B8√2π3C4√2π2D8√2π2
A direct current I=10A flows in a long straight round conductor. Find the magnetic flux through a half of the wire's cross-section per one meter of its length.
View SolutionSix long parallel current carrying wires are perpendicular to the plane of the fig. They pass through the vertices of a regular hexagon of side length a. All wires have same current I. Direction of current is out of the plane of the figure in all the wires except the one passing through vertex F, which has current directed into the plane of the figure. Calculate the magnetic induction field at the centre of the hexagon. Also tell the direction of the field.
 View Solution
View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)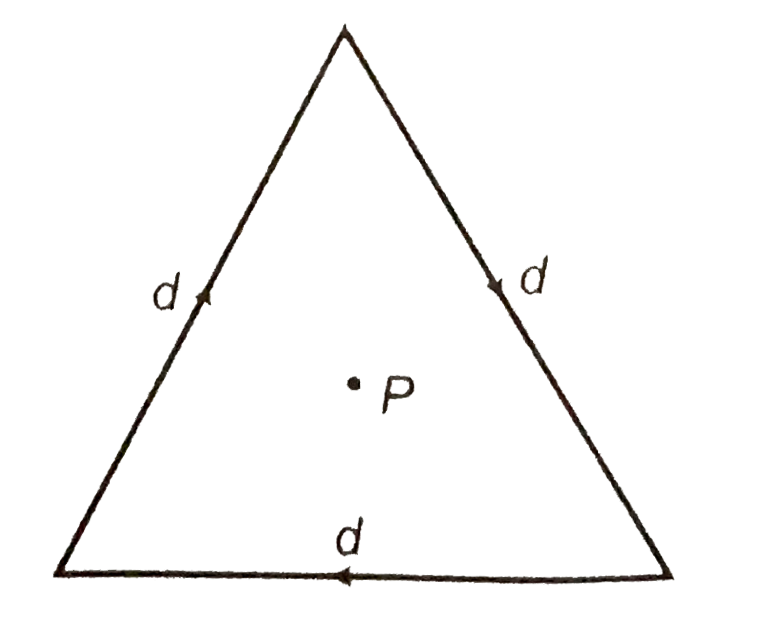
P is the centre of equilateral triangle.
(d)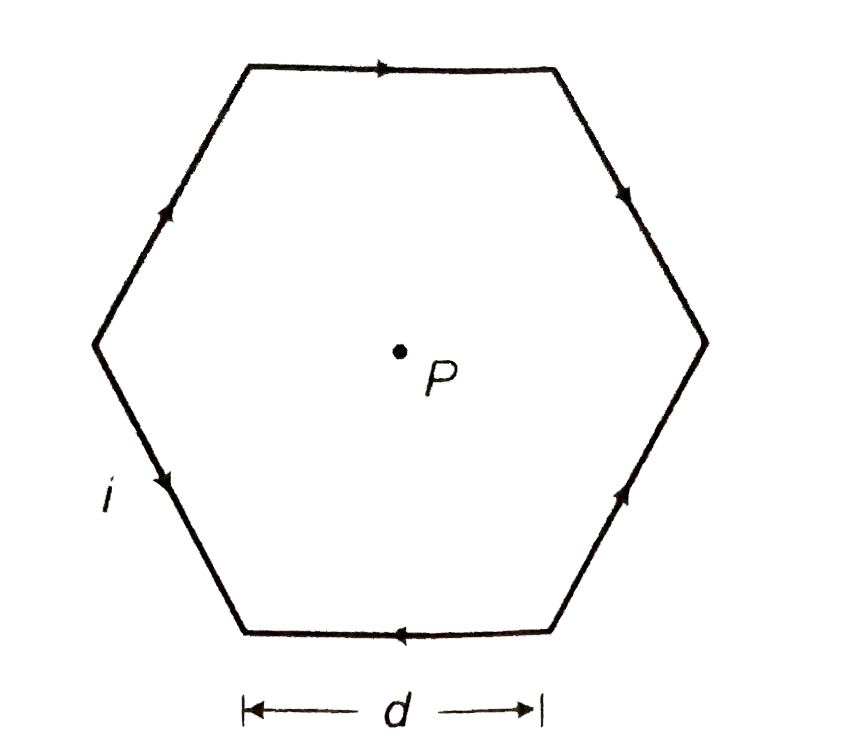
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)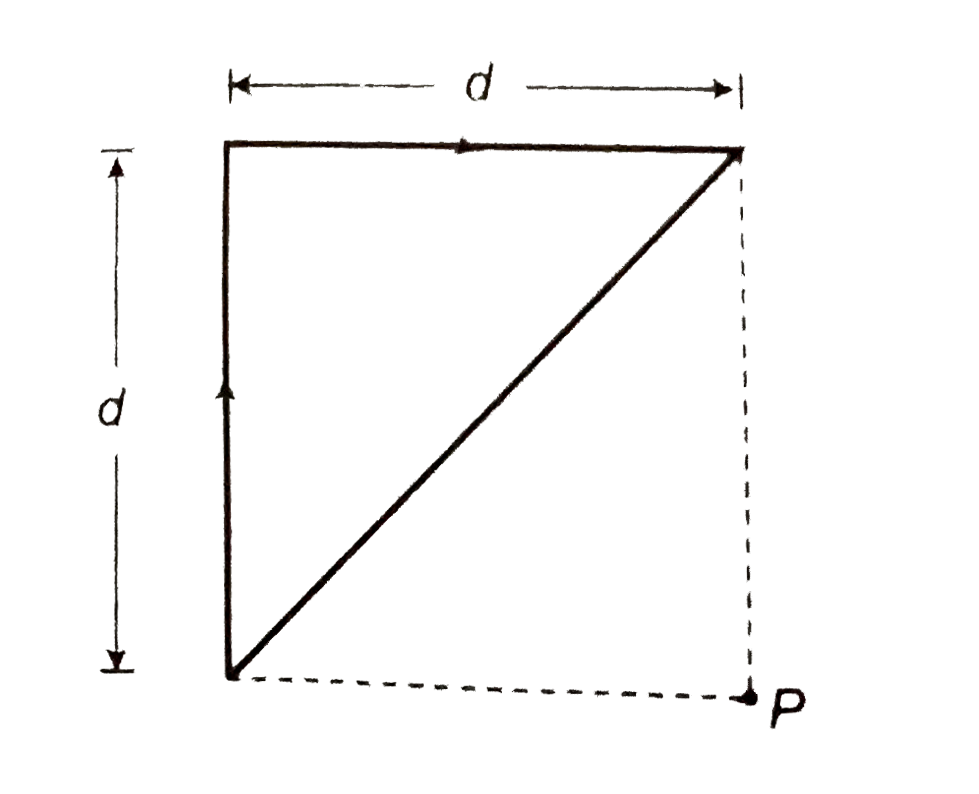
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.View SolutionA straight horizontal conducting rod of length l and mass m is suspended by two vertical wires at its ends. A current I is set up in the rod through the wires.
(i) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero.
(ii) What will be the total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before?View SolutionA light freely deformable conducting wire with insulation has its two ends (A and C) fixed to the ceiling. The two vertical parts of the wire are close to each other. A load of mass m is attached to the middle of the wire. The entire region has a uniform horizontal magnetic field B directed out of the plane of the figure. Prove that the two parts of the wire take the shape of circular arcs when a current I is passed through the wire. Neglect the magnetic interaction between the two parts of the wire.
 View Solution
View Solution

