The following objects are placed one after each other in given order onto a central axis with a separation of 40 cm each. A point source of light O. a diverging lens of focal length 40 cm. a converging lens of focal length 40 cm and converging mirror of focal length 80 cm. The aperture diameter of lenses and mirror is $d = 20 c m$ . If a point source of light is placed at a perpendicular distance of x from central axis then. (You have to consider single optical event at any optical element)
Mark the CORRECT statement(s):-

A

Height of final image is $\frac{x}{2}$

B

Height of final image is $\frac{x}{3}$

C

Image formed by converging lens is real and inverted

D

Image formed by converging mirror is real

Text Solution

Verified by Experts

The correct Answer is:A, C, D

Let us follow the way the images are formed by the lenses and the mirror. The virtual image formed by the diverging lens has an image distance of
$i_{1} = \frac{O_{1} f_{1}}{O_{1} - f_{1}} = \frac{- 4.4}{4 - (- 4)} d m = - 2 d m$ (dmrarrdecimeter)
Since the linear magnification is
$m_{1} = \frac{H_{i 1}}{H_{O 1}} = \frac{i_{1}}{O_{1}} = \frac{1}{2}$
the height of the first image is
$H_{i 1} = \frac{x}{2} = H_{O 2}$ .
This virtual image is seen by the diverging lens as an object with an object distance of $O_{2} = f_{2} + | i_{2} | = 6 d m$ , therefore the image formed by second lens has an image distance of
$i_{2} = \frac{O_{2} f_{2}}{O_{2} - f_{2}} = \frac{6.4}{6 - 4} d m = 12 d m$
The linear magnification of the second lens is
$m_{2} = \frac{i_{2}}{O_{2}} = \frac{12}{6} = 2$

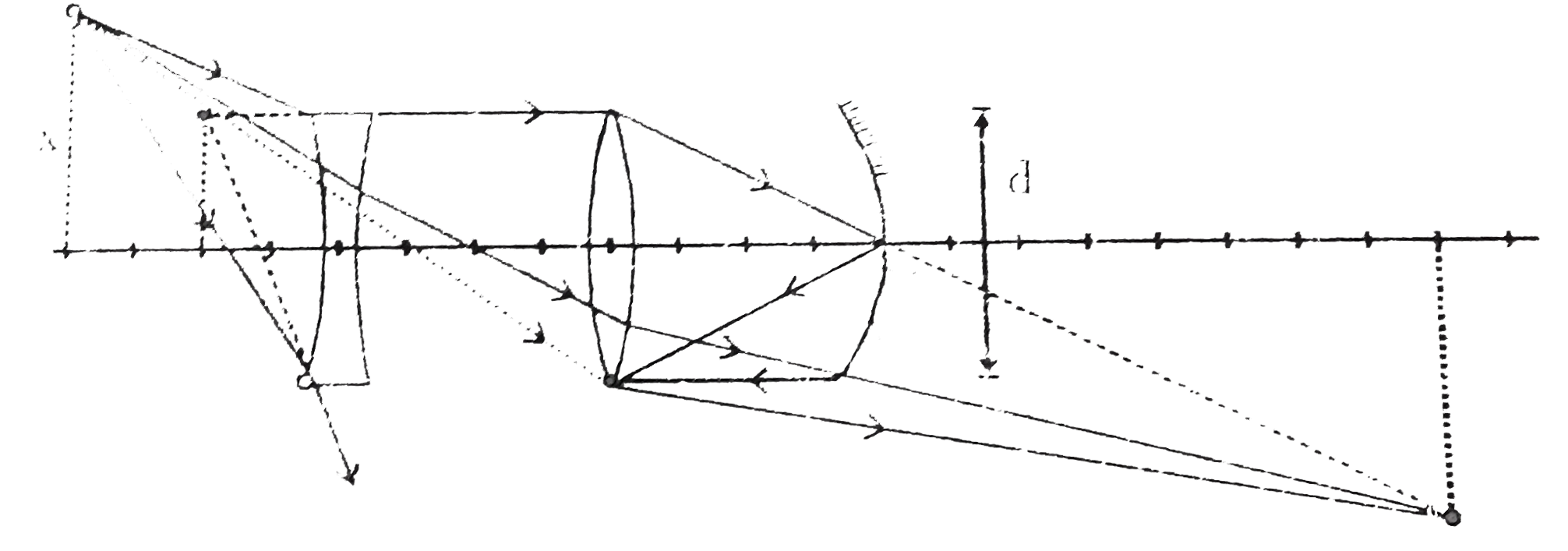
Hence the height of the second image is $H_{i 2} = m_{2} H_{O 2} = m_{2} H_{i 1} = x c = H_{O 3 .}$
The second image is seen by the concave mirror as a virtual object bering at a distance of $O_{3} = f_{3} - i_{2} = - 8 d m$ , therefore the image is formed at
$i_{3} = \frac{O_{3} f_{3}}{O_{3} - f_{3}} = \frac{- 8.8}{- 8 - 8} = \frac{- 64}{- 16} = 1 d m$
This is a real image and since the linear magnification of the mirror is:
$m_{3} = \frac{i_{3}}{O_{3}} = \frac{1}{2}$
the height of the final image is
$H_{i 3} = m_{3} H_{O 3} = \frac{x}{2}$
Note that final image is formed in the plane of the converging lens, therefore the image can only be captured on a screen if its height is greater than the radius of the lens. This happens when x is greater than d, therefore the list condition for perpendicular is d lt x. If x is increased further than $1.5 d$ , the rays will all pass under the concave mirror and there will be no image formation. Therefore the solution of the problem is :
$d < x < 1.5 d$ .creased further than $1.5 d$ , the rays will all pass under the concave mirror and there will be no images formation. Therefore the solution of the problem is:
$d < x < 1.5 d$ .

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

ALLEN-TEST PAPERS-part-2 physic

Home
Ask Doubt
Profile