A transverse harmonic wave travels along a taut string having a tension of 57.6N and linear mass density of 100g/m. Two points A and B on the string are 5 cm apart and oscillate with a phase difference of π6. How much does the phase of oscillation of point A change in a time interval of 5.0 ms?
The correct Answer is:2π5
Step by step video, text & image solution for A transverse harmonic wave travels along a taut string having a tension of 57.6 N and linear mass density of 100 g//m. Two points A and B on the string are 5 cm apart and oscillate with a phase difference of pi/6. How much does the phase of oscillation of point A change in a time interval of 5.0 ms? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A transverse harmonic wave is propagating along a taut string. Tension in the string is 50 N and its linear mass density is 0.02kgm–1 The string is driven by a 80Hz oscillator tied to one end oscillating with an amplitude of 1mm. The other end of the string is terminated so that all the wave energy is absorbed and there is no reflection
(a) Calculate the power of the oscillator.
(b) The tension in the string is quadrupled. What is new amplitude of the wave if the power of the oscillator remains same?
(c) Calculate the average energy of the wave on a 1.0m long segment of the string.
View SolutionA sinusoidal wave travels along a taut string of linear mass density 0.1g/cm. The particles oscillate along y-direction and the disturbance moves in the positive x-direction. The amplitude and frequency of oscillation are 2 mm and 50 Hz respectively. The minimum distance between two particles oscillating in the same phase is 4 m.
(a) Find the tension in the string.
(b) Find the amount of energy transferred through any point of the string in one second.
(c) If it is observed that the particle at x=2m is at y=1 mm at t=2s, and its velocity is in positive y-direction, then write the equation of this travelling wave.
View Solution
Knowledge Check
A transverse progressive wave on a stretched string has a velocity of 10ms−1 and a frequency of 100 Hz . The phase difference between two particles of the string which are 2.5cm apart will be
Aπ8Bπ4C3π)8Dπ2A transverse wave along a stretched string has a speed of 30 m/s and a frequency of 250 Hz. Then the phase difference between two points on the string 10 cm apart at the same instant is
A0Bπ/2 radC5π/3D8π/3A transerverse wave is travelling in x-direction a string having 5N and liner mass density 50gm/m. Shape of the string at a particular instant shown in figure. Both x and y are in meter angle 45∘ with x-axis. What is the speed of point P of string in m/s ?
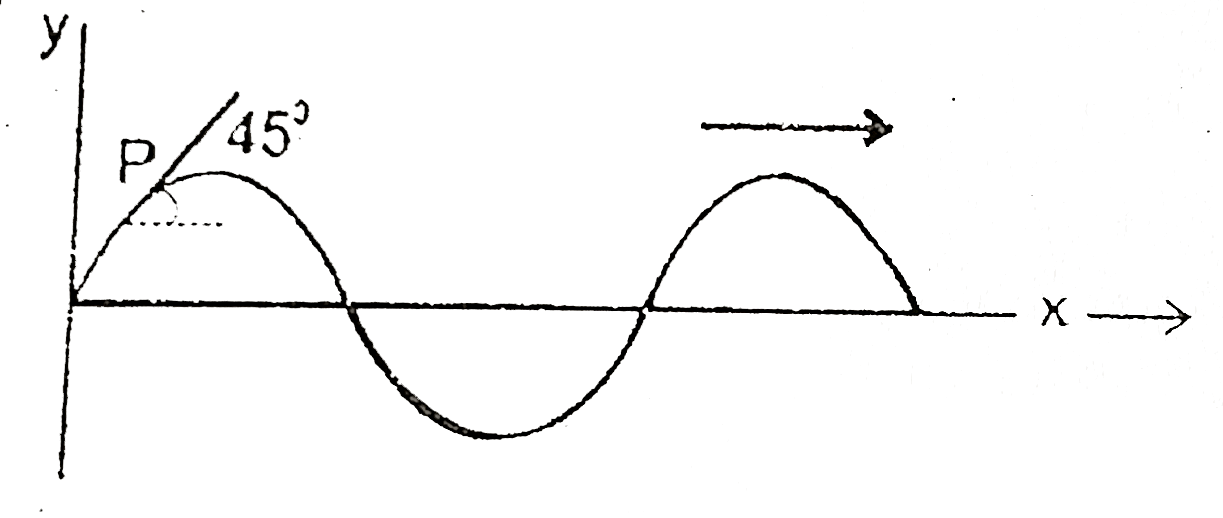 A10B5C0.5D1
A10B5C0.5D1
A transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
View SolutionTwo points A and B are at a distance of 30 cm on a stretched string. A travelling wave of frequency 300 Hz and velocity 100 m/s is set up in the string. What will be the phase difference between points A and B ?
View SolutionA sinusoidal wave travels along a taut string of linear mass density 0.1g/cm. The particles oscillate along y− direction and wave moves in the positive x− direction . The amplitude and frequency of oscillation are 2mm and 50Hz respectively. The minimum distance between two particles oscillating in the same phase is4m.
The amount of energy transferred ( in Joules ) through any point of the string in 5 seconds is
View SolutionA sinusoidal wave travels along a taut string of linear mass density 0.1g/cm. The particles oscillate along y− direction and wave moves in the positive x− direction . The amplitude and frequency of oscillation are 2mm and 50Hz respectively. The minimum distance between two particles oscillating in the same phase is4m.
The tension in the string is ( in newton )
View SolutionA sinusoidal wave travels along a taut string of linear mass density 0.1g/cm. The particles oscillate along y− direction and wave moves in the positive x− direction . The amplitude and frequency of oscillation are 2mm and 50Hz respectively. The minimum distance between two particles oscillating in the same phase is4m.
If at x=2m and t=2s, the particle is at y=1mm and its velocity is in positive y− direction, then the equation of this travelling wave is :(y is in mm,t is in seconds and x is in metres )
View Solution
