A metal cylinder of radius R is placed on a wooden plank BD. The plank is kept horizontal suspended with the help of two identical string AB and CD each of length L. The temperature coefficient of linear expansion of the cylinder and the strings are a1 and a2 respectively. Angle q shown in the figure is 30∘. It was found that with change in temperature the centre of the cylinder did not move. Find the ratio α1α2 , if it is know that L = 4R. Assume that change in value of θ is negligible for small temperature changes

The correct Answer is:α1α2=81
Topper's Solved these Questions
Similar Questions
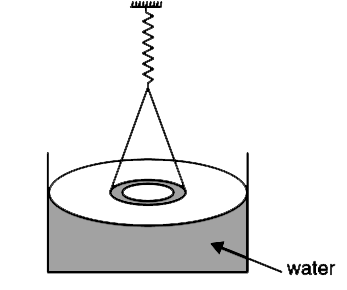
A circular ring has inner and outer radii equal to 10mmand30mm respectively Mass of the ring is m=0.7 g. It gently pulled out vertically from a water surface by a sensitive spring. When the spring is stretched 3.4cm from its equilibrium position the ring is on verge of being pulled out from the water surface. If spring constant is k=0.7Nm–1 find the surface tension of water.
View SolutionDuring a painting process, a thin, flat tape of width b (dimension perpendicular to the plane of the figure) is pulled through a paint filled channel of length L. The density and viscosity of the paint liquid is ρ and η respectively. The tape is pulled at a constant speed v and width of the channel is h. Find the minimum force needed to pull the tape.

View Solution
A cylinder of radius R is to roll without slippoing between two planks as shown in the figure. Then
View Solution
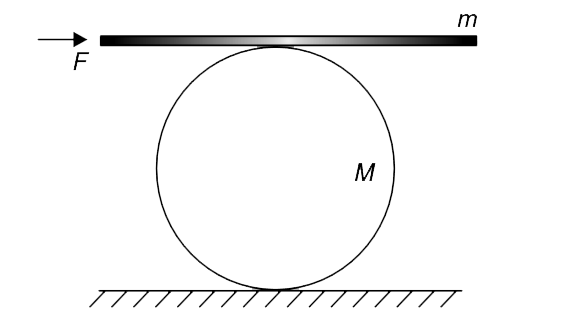
A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
View SolutionA cylinder is rolling without slipping on a horizontal plane P. The friction between the plank P and the cylinder is sufficient for no slipping. The coefficient of friction between the plank and the ground surface is zero. Initially, P is attached with a string S as shown in the figure. If the string is now burned, then.
View SolutionA plank of length 20 m and mass 1kg is kept on a horizontal smooth surface. A cylinder of mass 1lg is kept near one end of the plank. The coefficient of friction between the two surface is 0.5 . The plank is suddenly given a velocity 20 m//s towards left Time in which plank and cylinder separate
View SolutionConsider a cylinder of mass M=1 kg and radius R=1 m lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure. A force F=55N is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact. The acceleration of cylinder is
View Solutiona point charge q is placed at the centre of a cylinder of length L and radius R the electric flux through the curved surface of the cylinder is
View SolutionA boy pushes a cylinder of mass M with the help of a plank of mass m as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find
(a) The acceleration of the centre of the cylinder
(b) The friction force between the plank and the cylinder
View SolutionAB is a non uniform plank of length L = 4R with its centre of mass at C such that AC = R . It is placed on a step with its one end A supported by a cylinder of radius R as shown in figure. The centre of mass of the plank is just outside the edge of the step. The cylinder is slowly rolled on the lower step such that there is no slipping at any of its contacts. Calculate the distance through which the centre of the cylinder moves before the plank loses contact with the horizontal surface of the upper step.
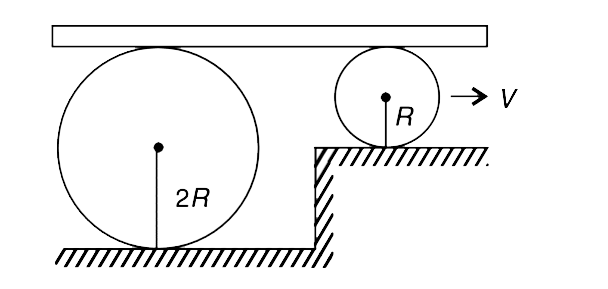
View SolutionIn the figure the plank resting on two cylinders is horizontal. The plank is pulled to the right such that the centre of smaller cylinder moves with a constant velocity v. Friction is large enough to prevent slipping at all surfaces. Find-
(a) The velocity of the centre of larger cylinder.
(b) The ratio of accelerations of the points of contact of the two cylinders with the plank.
View SolutionIn the figure shown a plank of mass m is lying at rest on a smooth horizontal surface. A cylinder of same mass m and radius r is rotated to an angular speed w0 and then gently placed on the plank. It is found that by the time the slipping between the plank and the cylinder cease, 50% of total kinetic energy of the cylinder and plank system is lost. Assume that plank is long enough and um is the coefficient of friction between the cylinder and the plank.
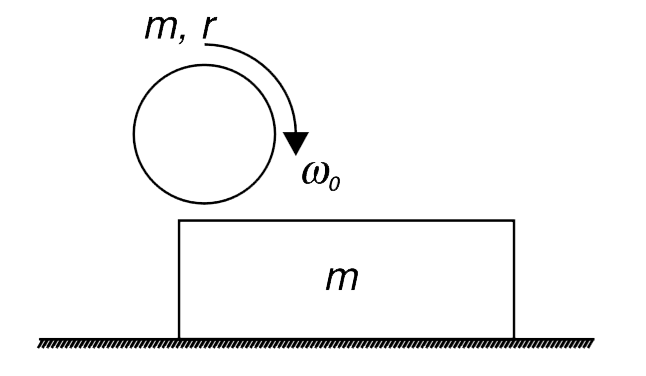
(a) Find the final velocity of the plank.
(b) Calculate the magnitude of the change in angular momentum of the cylinder about its centre of mass.
(c) Distance moved by the plank by the time slipping ceases between cylinder and plank.
View SolutionA plank of mass M is placed on a smooth surface over which a cylinder of mass m and radius R is placed as shown in figure-5.63. Now the plank is pulled towards right with an external force F. If cylinder does not slip over the surface of plank find the linear acceleration of plank and cylinder and the angular acceleration of the cylinder.
View SolutionA thin but very large plank of mass 2 m is placed on a horziontal smooth surface. A solid cylinder of mass m and radius r is given only translational velocity v_(0) and gently placed on the plank as shown in the figure. The coefficient of kinetic friciton between the plank and the cylinder is mu .
View SolutionPassage - II :
A solid cylinder of mass m and radius R and that of plank M placed on smooth horizontal surface. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder. If plank is pulled force F. answer the following

The acceleration of the cylinder is
View Solution
