A uniform rope tightly wraps around a uniform thin ring the mass M and radius R. The mass of the segment of the rope around the ring (i.e. , mass of the length2πR of the rope) is also M. The ends of the rope are fixed one above the other and it is taut. The ring is let go. Find its acceleration. Assume no slipping and thickness of the rope to be negligible.
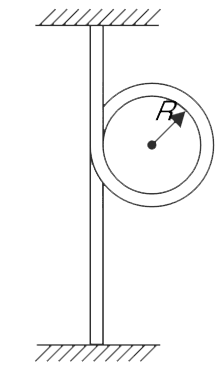
The correct Answer is:g2
Step by step video, text & image solution for A uniform rope tightly wraps around a uniform thin ring the mass M and radius R. The mass of the segment of the rope around the ring (i.e. , mass of the length2 pi R of the rope) is also M. The ends of the rope are fixed one above the other and it is taut. The ring is let go. Find its acceleration. Assume no slipping and thickness of the rope to be negligible. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Moment of inertia of a uniform circular ring of mass M and radius R about a diameter of ring is………………. .
View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR - Question 2 - Select One
A rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
AMRFBMRFCRMFDFMR - Question 3 - Select One
A rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
AF/MRBM/F RCR/MFDMR/F
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionA massless rope is wrapped around a ring (with a groove along its circumference) having radius R and mass m. The ring is allowed to move download. The linear acceleration of the ring is
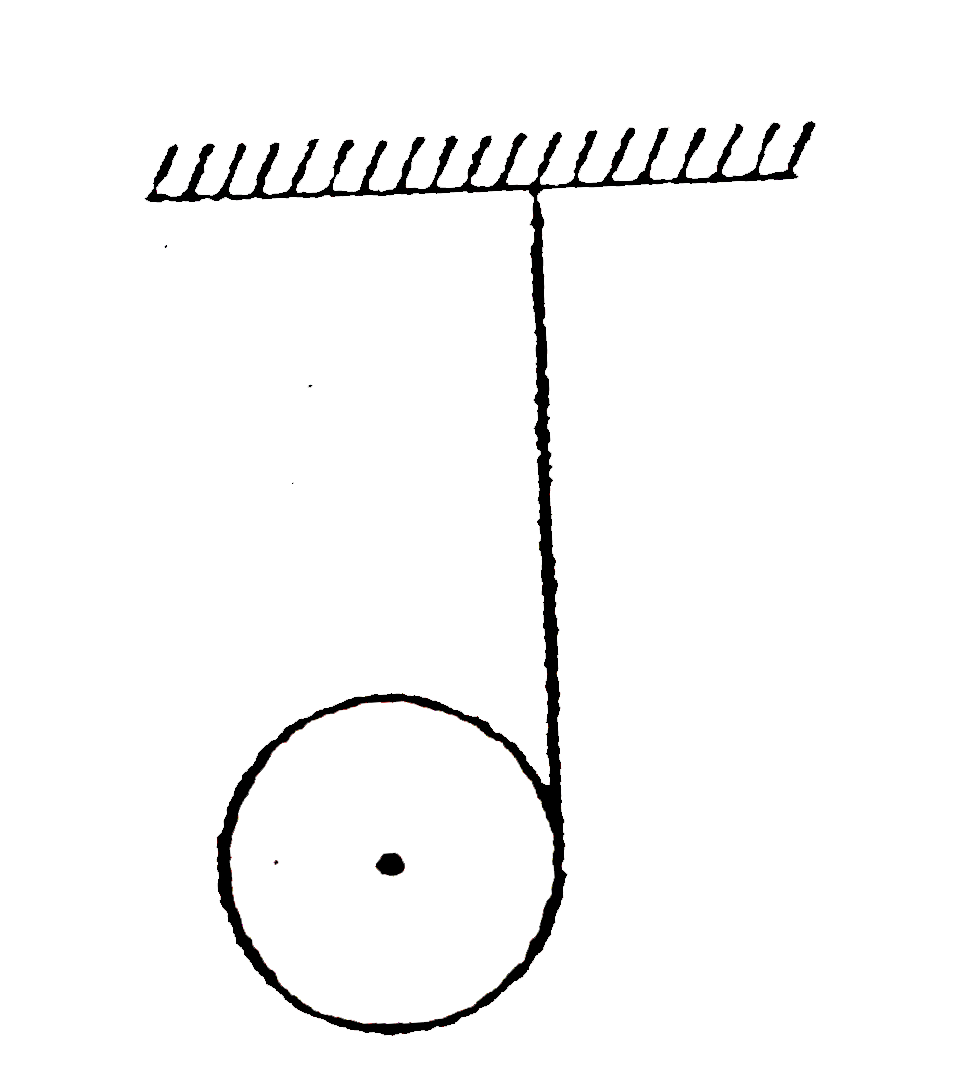 View Solution
View SolutionA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View SolutionA rope is wound round a hollow cylinder of mass 2 kg and radius 0.5 m. If the rope is pulled with a force of 80 N, the angular acceleration of the cylinder will be -
View Solution

