In the last question let us assume that the uniform electric field makes an angle θ with the vertical in downward direction. With the uniformly charged rod in vertical position the field is switched on. Mass of the rod, its length and charge per unit length is M, L and λ respectively. (a) Find the strength of field (E) such that the rod can reach the horizontal position if θ=30∘ (b) Find the minimum strength of field (E) such that the rod can reach the horizontal position if θ=60∘ (c) However high the field might be, the rod cannot become horizontal if θ<θ0 find θ0

The correct Answer is:(a) Not possible
(b). E=(2√3−1)MgλL
(c) θ0=45∘
Topper's Solved these Questions
Similar Questions
Two unequal masses, m1=2m and m2=m have unequal positive charge on them. They are suspended by two mass-less threads of unequal lengths from a common point such that, in equilibrium, both the masses are on same horizontal level. The angle between the two strings is θ=45∘ in this position. Find the Electrostatic force applied by m1 on m2 in this position.

View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
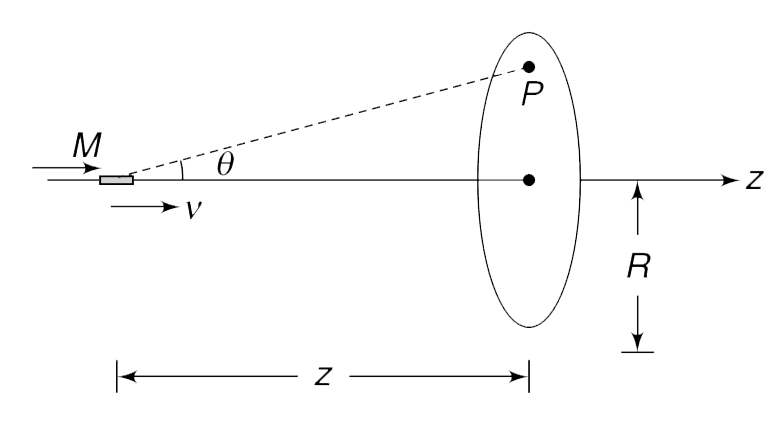
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.
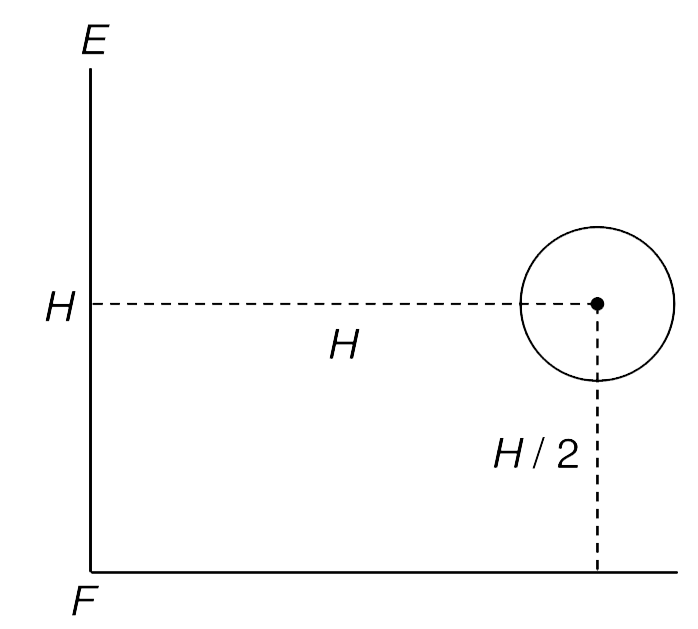
View SolutionIn the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle theta from the vertical.
View SolutionA conical pendulum, a thin uniform rod of length l and mass m , rotates uniformly about a vertical axis with angular velocity omega (the upper end of the rod is hinged). Find the angle theta between the rod and the vertical.
View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA thin uniform rod of mass M and length 2L is hinged at its centre O so that it can rotate freely in horizontal plane about the vertical axis through O. at its ends the insulating rod has two point charges 2q and q (see figure). An electrif field E is switched on making and angle theta_(0)=60^(@) with the initial position of the rod. The field is uniform and horizontal. (a) Calculate the maximum angular velocity of the rod during subsequent motion. (b) Find the maximum angular acceleration of the rod.
View SolutionA uniformly charged non conducting rod is suspended vertically at its end. The rod can swing freely in the vertical plane without any friction. The linear charge density on the rod is lamda C//m and it has a uniformly distributed mass of M Length of the rod is L. A uniform horizontal electrif field (E) is switched on in the region. (a). For what value of electric field (call it E_(0) ) the rod just manages to make itself horizontal.? (b). If eletrif field E_(0) is switched on, what is the maximum angular speed acquired by the rod during its motion?
View SolutionA rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle theta with the vertical.
View SolutionA rod of length l is moved horizontally with a uniform velocity v in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive an expression for the emf induced across the ends of the rod.
View SolutionA uniform rod of mas m and length l is made to stand at an angle of 60∘ with the vertical. What is the potential energy of the rod in this position?
View SolutionUniform magnetic field B, exists in the vertical downward direction. A rod whose length is kept horizontal and is moved with velocity v perpendicular to its length. Motional emf developed across the length of the rod is
View SolutionFigure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is lambda . Find the electric field due to the rod at a point P which is at a distance r from the rod.
View Solution
