![(a). Use the method in part (b) of the previous problem of calculate the electrostatic self energy of a uniformly charegd sphere of radius R having charge Q. (b). Divide the above sphere (mentally) into two regions-spherical concentric part having radius (R)/(2) and the remaining annular part (between (R)/(2) and R). Denote the point charges in sphere of radius R//2 by q(1),q(2),q(3) .. . .etc. The charges in annular part be denoted by Q(1),Q(2),Q(3) . . . etc. Calculate the electrostatic interaction energy for all pairs like [(Q(i),Q(j))+(q(i)+q(j))].](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V02_C06_E01_160_Q01.png)
(a). Use the method in part (b) of the previous problem of calculate the electrostatic self energy of a uniformly charegd sphere of radius R having charge Q.
(b). Divide the above sphere (mentally) into two regions-spherical concentric part having radius R2 and the remaining annular part (between R2 and R). Denote the point charges in sphere of radius R/2 by q1,q2,q3 .. . .etc.
The charges in annular part be denoted by Q1,Q2,Q3 . . . etc.
Calculate the electrostatic interaction energy for all pairs like [(Qi,Qj)+(qi+qj)].
The correct Answer is:(a). 35Q24πε0R
(b). 147320Q24πε0R
Topper's Solved these Questions
Similar Questions
Two unequal masses, m1=2m and m2=m have unequal positive charge on them. They are suspended by two mass-less threads of unequal lengths from a common point such that, in equilibrium, both the masses are on same horizontal level. The angle between the two strings is θ=45∘ in this position. Find the Electrostatic force applied by m1 on m2 in this position.
03:51View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
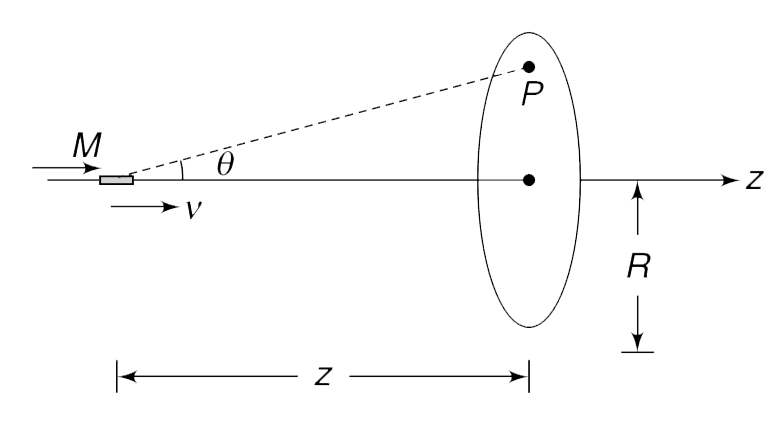
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.03:01View SolutionIn the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
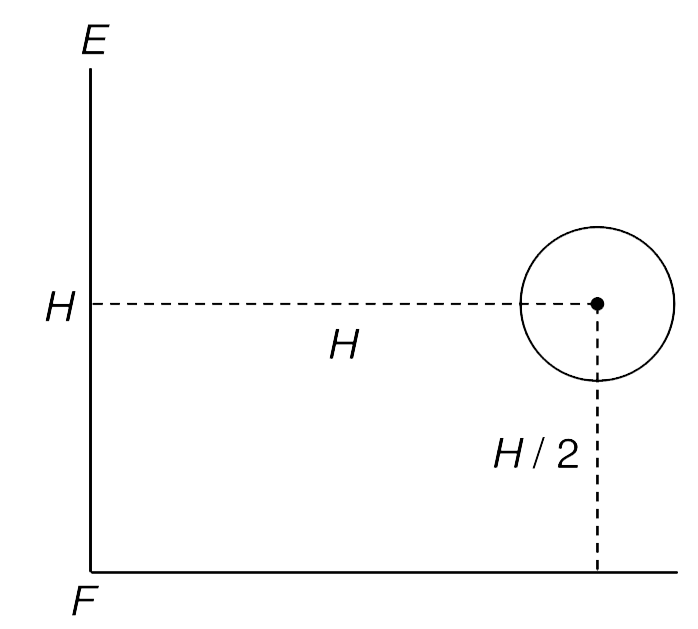03:07View SolutionA small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is positive, charge will necessilly flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2 on the shell is [Fig]
04:43View SolutionIn figure , a solid sphere of radius a = 2.00cm is concentric with a spherical conduction shell of inner radius b =2.00 a and outer radius c=2.40 a. the sphere has a net uniform charge q1=+5.00C. The shell has a net charge q2=−q1. Distance (a) r=0 (b) r= a/2.00 (c) r=a (d) r = 1.50 a (e) r= 2.30a and (f) r= 3.50 a ? what si the net charge on the (g) inner and (h) outer surface of the shell ?
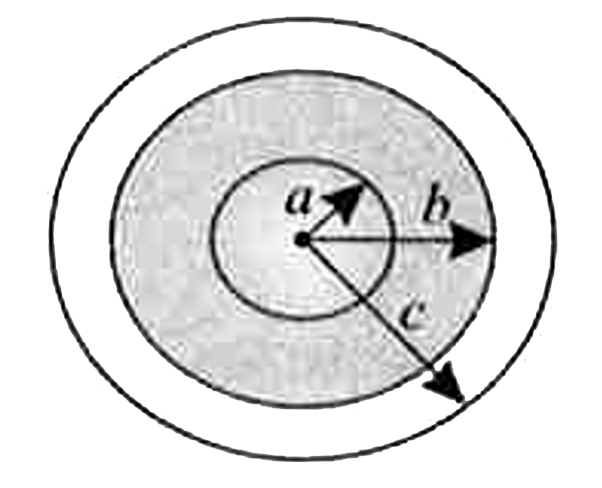02:23View Solutionधातु के बने R,2R तथा 3 R त्रिज्याये वाले तीन खोखले सेकेंडरी गोलों को क्रमशः Q1,Q2 तथा Q3 आवेश दिए जाते है तीनो गोले की बाहरी सतह पर आवेश के घनत्व बराबर पाए जाते है तब दिए गए आवेशों का अनुपात Q1:Q2:Q3 होगा
01:17View SolutionA charge q_(1) is placed at the centre of a spherical conducting shell of radius "R" .Conducting shell has a total charge q_(2) .Electrostatic potential energy of the system is (A) (q_(1)^(2)+2q_(1)q_(2))/(8 pi varepsilon_(0)R) (B) (q_(2)^(2)+2q_(1)q_(2))/(8 pi varepsilon_(0)R) (C) (q_(1)^(2)+q_(1)q_(2))/(8 pi varepsilon_(0)R) (D) (q_(2)^(2)+q_(1)q_(2))/(8 pi varepsilon_(0)R)
04:46View Solutionदो सकेंद्रिय गोलीय खेलो को जिनकी त्रिज्याएँ R और 2R है, क्रमशः Q1 और Q2 आवेश दिए गए है। खोलो में पृष्ठ आवेश घनत्व समान है। Q1Q2 की गणना कीजिए।
03:03View SolutionIn the following question a statement of assertion (A) is followed by a statement of reason (R ) A : Two large conducting spheres carrying charges Q_(1) and Q_(2) are brought close to each other. The magnitude of electrostatic force between them is exactly given by Q_(1) Q_(2)// 4 pi epsilon_(0) r^(2) , where r is the distance between their centres. R: Here charges Q_(1) and Q_(2) can be assumed to be concentrated at the centres of their respective spheres.
View SolutionTwo concentric spheres of raddi R and r have positive charges q1andq2 with equal surface charge densities. What is the electric potential at their common centre?
03:46View SolutionA small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radium r2 and charge q2. Show that if q1 is positive , charge will neecessarily flow from the sphere to the shell ( when the two are connected by a wire ) no matter what the charge q2 on the shell is .
05:10View SolutionA small sphere of radius r_(1) and charge q_(1) is enclosed by a spherical shell of radius r and charge q_(2) Show that if q_(1) is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q_(2) on the shell is.
02:46View SolutionA small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radius r and charge q2 Show that if q1 is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2 on the shell is.
View SolutionA small sphere of radius r_(1) and charge q_(1) is enclosed by a spherical shell of radius r and charge q_(2) Show that if q_(1) is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q_(2) on the shell is.
View SolutionA small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2 on the shell is [Fig]
07:42View SolutionQ आवेश को दो भागों Q1 तथा Q2 में विभाजित करके, उन्हें R दूरी पर रखा जाता है होगा। यदि : -
03:33View Solution