A proton beam has a circular cross sectional area A and it carries a current I distributed uniformly over its cross section. Calculate the magnetic energy per unit length of the beam within the beam.
The correct Answer is:μ0I216π
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2
39 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- CURRENT ELECTRICITYBOOK - ARIHANTCHAPTER - CURRENT ELECTRICITYEXERCISE - Current Electricity
105 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
Similar Questions
A rectangular conducting loop PQRS is kept in xy plane with its adjacent sides parallel to x and y axes. A mag- netic field →B is switched on in the region which varies in posi- tion and time as →B=[B0sin(ky–ωt)]ˆk . It was found that the emf induced in the loop is always zero. Express the length (L) of the loop in terms of constant k and ω.

View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
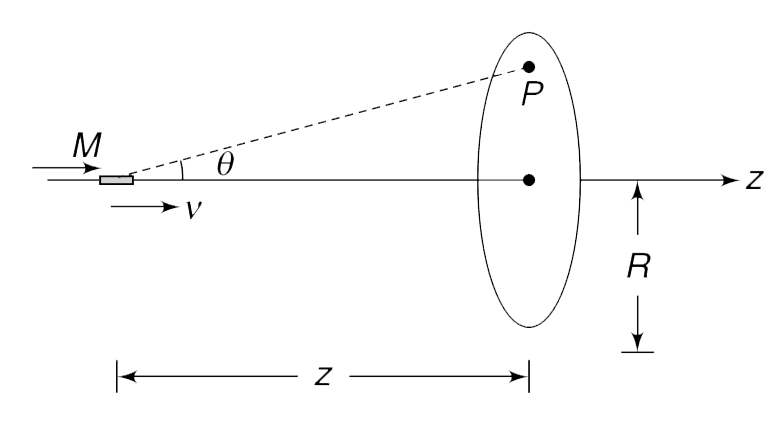
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.
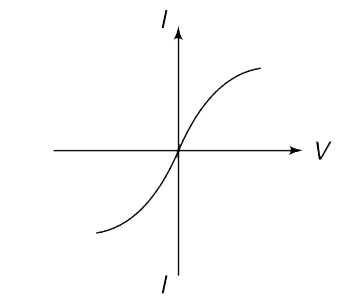
View SolutionThe current-voltage graph for a resistor is as shown in the figure. Is it right to say that resistance decreases as the current through it increases ?
View SolutionThree small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA 1μA beam of protons with a cross - sectional area of 0.5sq.mm is moving with a velocity of 3×104ms−1 . Then charge density of beam is
View SolutionIn a particle accelerator, a current of 500muA is carried by a proton beam in which each proton has speed of 3xx10^(7)m//s . The cross sectional area of the beam is 1.50mm^(2) . The charge density in this beam in Coulomb/m3 is close to
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionAn electron beam has an aperture of 1.0 mm^(2) . A total of 6xx10^(16) electrons flow through any perpendicular cross-section per second. Calculate (i) the current (ii) the current density in the electron beam.
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of circular cross section is Made of non-Magnetic Material.The wire of radius (a).The wire carries a current (I) which is uniformly distributed over its cross-section.The energy stored per unit length in Magnetic field contained within the wire.
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross - section (radius a) carrying steady current I. The current I is uniformly distributed across this cross - section . Calculate the magnetic field in the region r lt a and r gt a
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r a.
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View Solution
