A sample of radioactive material has an alpha emitter (X) and a beta emitter (D). The energy of decay reactions are Q1 and Q2 respectively.
.AZX→.A−4Z−2Y+.42He+Q1
.A'Z'D→.A'Z'+1B+.0−1e+→v+Q2
The radiation coming out from the sample is passed through two parallel slits S1 and S2 to get a narrow parallel beam to alpha and beta particles. This beam is allowed to enter perpendicularly into a region of inform magnetic field. The particles after taking a semicircular path strike the screen at a point a above the line L and, below the line L particles are found to strike the screen everwhere from O to b. the distance Oa and Ob and r1 and r2 respectively. Find the ratio r1r2.
Take Q1Q2=k and assume that mass of alpha particles is 4 time the mass of a proton which is η times the mass of an electron.
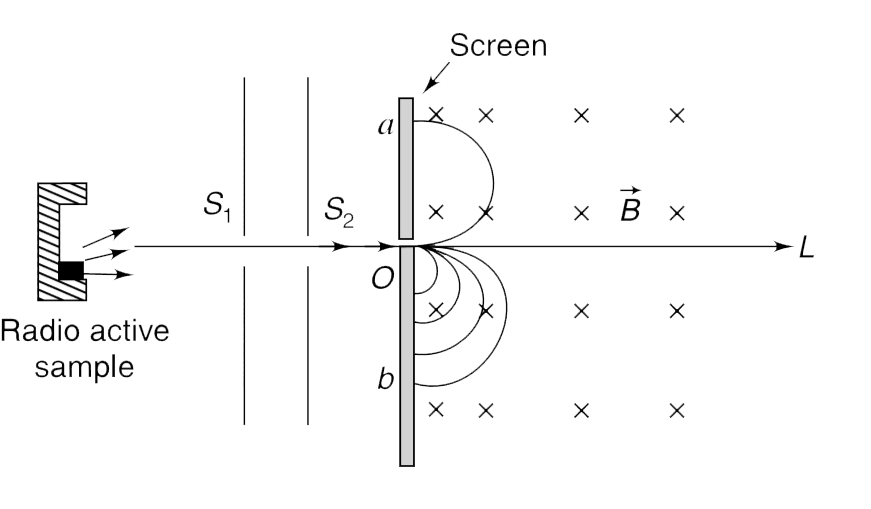
The correct Answer is:r1r2=√πk(A−4A)
Topper's Solved these Questions
Similar Questions
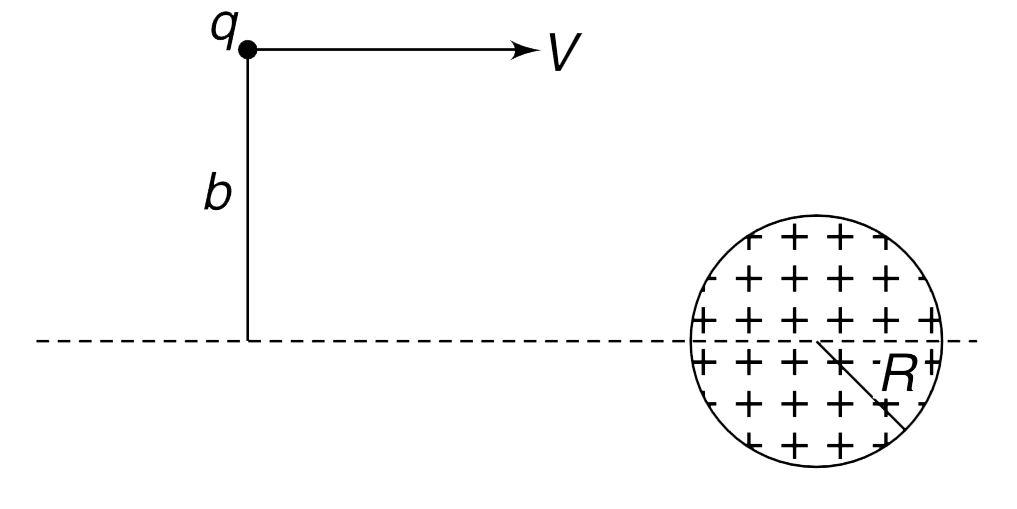
There is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
View SolutionIn the figure shown M represents a mirror. AB is an incident wavefront. Which type of mirror is M if the reflected wave front
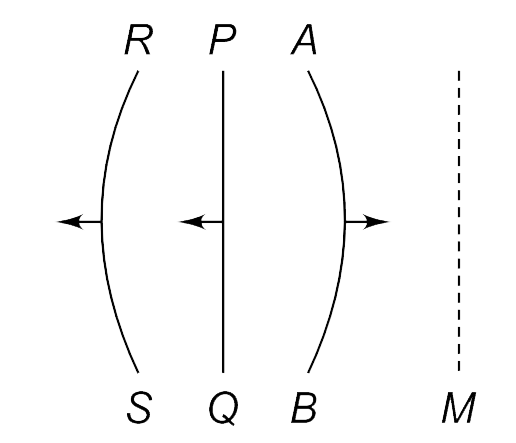
(a)PQ (b)RS
View SolutionTwo charges +q_(1) and -q_(2) are placed at A and B respectively. A line of force emanates from q_(1) at an angle alpha with the line AB. At what angle will it terminate at -q_(2) ?
View SolutionIn plate A has 100 muC charge, while plate B has 60 muC charge. a. When both switches are open, then q_(1)="_____" q_(2)="______" q_(3)="______" q_(4)="_______" b. When switch S_(1) is closed, the q_(1)="_____" , q_(2)="______" q_(3)="_______" , q_(4)="_____" c. When switch S_(1) is also closed, then q_(1)="______" q_(2)="______" q_(3)="______" ltbrlt q_(4)="_______" . .
View SolutionTwo large , parallel conducting plates X and Y , kept close to each other , are given Q1 and Q2(Q1>Q2). The four surfaces of the plates are A,B,C and D , as shown

(i) The charge on A is 12(Q1+Q2)
(ii) The charge on B is 12(Q1−Q2)
(iii) The charge on C is 12(Q2−Q1)
(iv) The charge on D is 12(Q1+Q2)
View SolutionAn electrostatic field line leaves at an angle alpha from pint change q_(1) and connects with point charge -q_(2) at an angle beta ( q_(1) and q_(2) are positive) (see figure below). If q_(2)=3/2 q_(1) and alpha=30^(@) , then
View Solutionif x,y and z are not all zero and connected by the equations a1x+b1y+c1z=0,azx+b2y+c2z=0 and (p1+λq1)x+(p2+λq2)y+(p3+λq3)z=0 show that
λ=−∣∣ ∣ ∣∣a1b1c1a2b2c2p1p2p3∣∣ ∣ ∣∣÷∣∣ ∣ ∣∣a1b1c1a2b2c2q1q2q3∣∣ ∣ ∣∣
View SolutionA reaction proceeds through two paths I and II to convert X rarr Z . What is the correct relationship between Q. Q_(1) and Q_(2) ?
View SolutionIf q1,2,q3 are roots of the equation x3+64=0, then the value of ∣∣ ∣ ∣∣q1q2q3q2q3q1q3q1q2∣∣ ∣ ∣∣ is :-
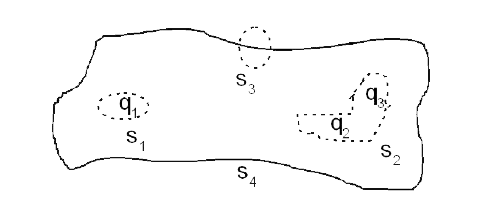
View SolutionThree charges q1=1μc,q2=2μc and q3=−3μc and four surfaces S1,S2,S3 and S4 are shown. The flux emerging through surface S2 in N−m2/C is-
View Solution[" Two uniformly charged non "],[" conducting spheres of radii "R_(1)" and "],[R_(2)" having charges "Q_(1)" and "Q_(2)],[" respectively are seperated by "],[" distance "r" .Total electrostatic "],[" energy of this system is "],[qquad [U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))+(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))-(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))-(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(R_(2))+(Q_(1)Q_(2))/(r)}]]
View SolutionIf Q1,Q2,Q3,Q4 are the quadrants in a Cartesian plane then Q2∩Q3 is ________.
View Solutionif x,y and z are not all zero and connected by the equations a1x+b1y+c1z=0,azx+b2y+c2z=0 and (p1+λq1)x+(p2+λq2)y+(p3+λq3)z=0 show that
λ=−∣∣ ∣ ∣∣a1b1c1a2b2c2p1p2p3∣∣ ∣ ∣∣÷∣∣ ∣ ∣∣a1b1c1a2b2c2q1q2q3∣∣ ∣ ∣∣
View SolutionIf q1,q2,q3 ar rootsof the equation x3+64=0 then value of ∣∣ ∣ ∣∣q1q2q3q2q3q1q3q1q2∣∣ ∣ ∣∣
View SolutionA reaction proceeds through two paths I and II to convert X→Z.

What is the correct relationship between Q.Q1andQ2 ?
View Solution
