A long cylindrical conductor of radius R has two cylindrical cavities of diameter R through its entire length, as shown in the figure. There is a current I through the conductor distributed uniformly in its entire cross section (apart from the cavity region). Find magnetic field at point P at a distance r=2R from the axis of the conductor (see figure).

The correct Answer is:B=934μ0IπR
Topper's Solved these Questions
Similar Questions
A long cylindrical conductor of radius a has two cylindrical cavities of diameter a through its entire length as shown in cross-section in figure. A current I is directed out of the page and is uniform throughout the cross-section of the conductor. Find the magnitude and direction of the magnetic field in terms of μ0,I,r and a.
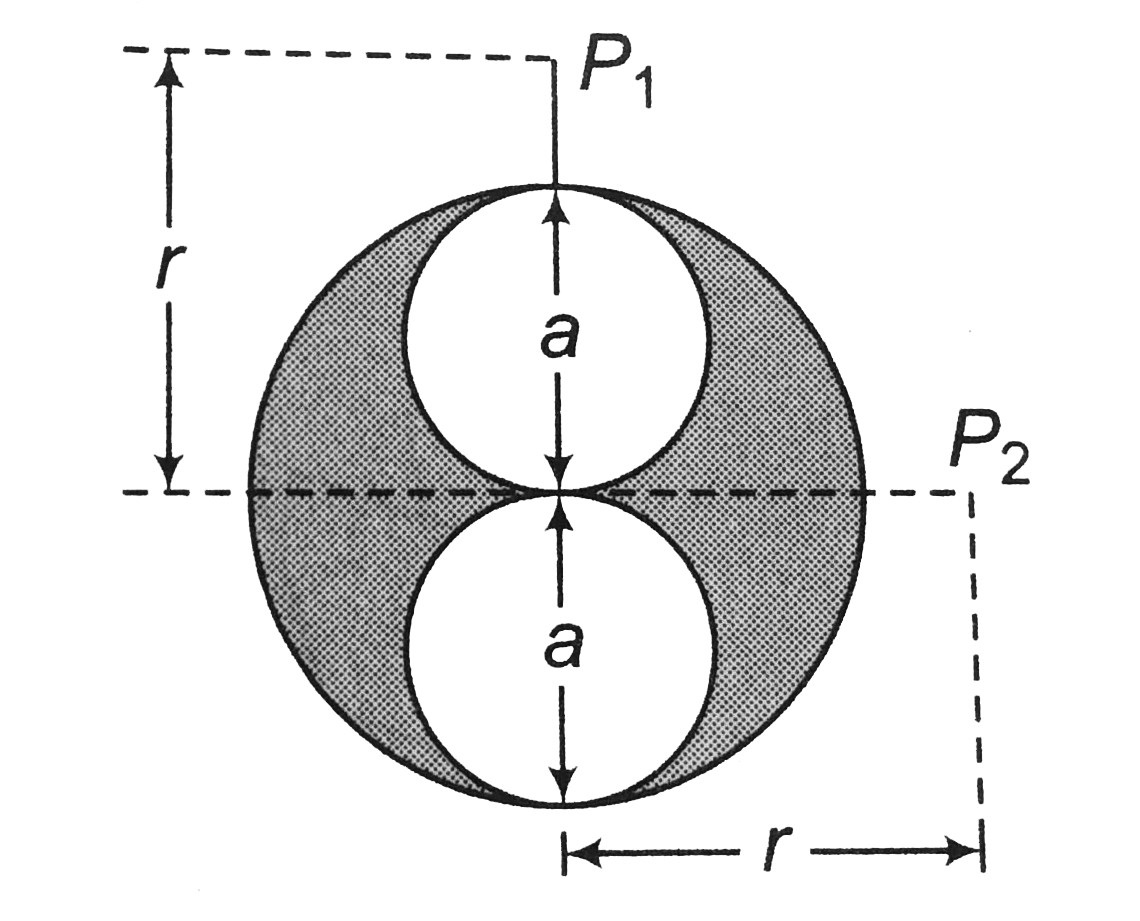
(a) at point P1 and (b) at point P2
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View Solution
Knowledge Check
Current flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
AB=0 at the axisBB∝x for 0≤x≤rCB∝1/x for x>rDB is maximum for x=rA long, thick straight conductor of radius R carries current I uniformly distributed in its cross section area.The ratio of energy density of the magnetic field at distance R/2 from surface inside the conductor and outside the conductor is:
A1:16B1:1C1:4D9/16A long cylindrical conductor of radius R having a cylindrical cavity of radius R/2 through out its length is lying with its axis parallel to x-axis. The distance between the axes of the cylinder and the cavity length in the positive x direction. The across sectional view of the cylinder is shown in the figure

The magnetic induction at point on the cavity isAμ0I3πR(−ˆl)Bμ0i3πR(ˆk)Cμ0i6πR(ˆj)Dμ0I6πR(−ˆj)
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA long, thick straight conductor of radius R carries current I uniformly distributed in its cross section area.The ratio of energy density of the magnetic field at distance R/2 from surface inside the conductor and outside the conductor is:
View Solution
