Two identical coils having radius R and number of turns N are placed co-axially with their centres separated by a distance equal to their radius R. The two coils are given same current I in same direction. The configuration is often known as a pair of Helmholtz coil.
(i) Calculate the magnetic field (B) at a point (P) on the axis between the coils at a distance x from the centres of one of the coils.
(ii) Prove that dBdx=0 and d2Bdx2=0 [ In fact d3Bdx3 is also equal to zero ] at the point lying midway between the two coils. What conclusion can you draw from these results?
![Two identical coils having radius R and number of turns N are placed co-axially with their centres separated by a distance equal to their radius R. The two coils are given same current I in same direction. The configuration is often known as a pair of Helmholtz coil. (i) Calculate the magnetic field (B) at a point (P) on the axis between the coils at a distance x from the centres of one of the coils. (ii) Prove that (dB)/(dx) = 0 and (d^(2)B)/(dx^(2)= 0 [ In fact (d^(3)B)/( dx^(3)) is also equal to zero ] at the point lying midway between the two coils. What conclusion can you draw from these results?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V02_C10_E01_025_Q01.png)
The correct Answer is:(1)μ0NIR22⎡⎢ ⎢ ⎢⎣1(R2+x2)3/2+1R2+(R−x2]3/2 (2) The magnetic field is constant at points close to mid way between the coils.
Topper's Solved these Questions
Similar Questions
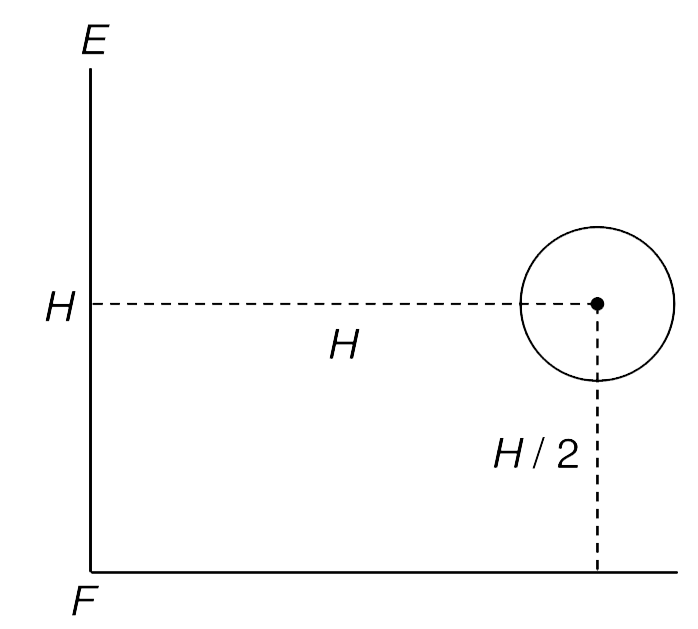
In the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
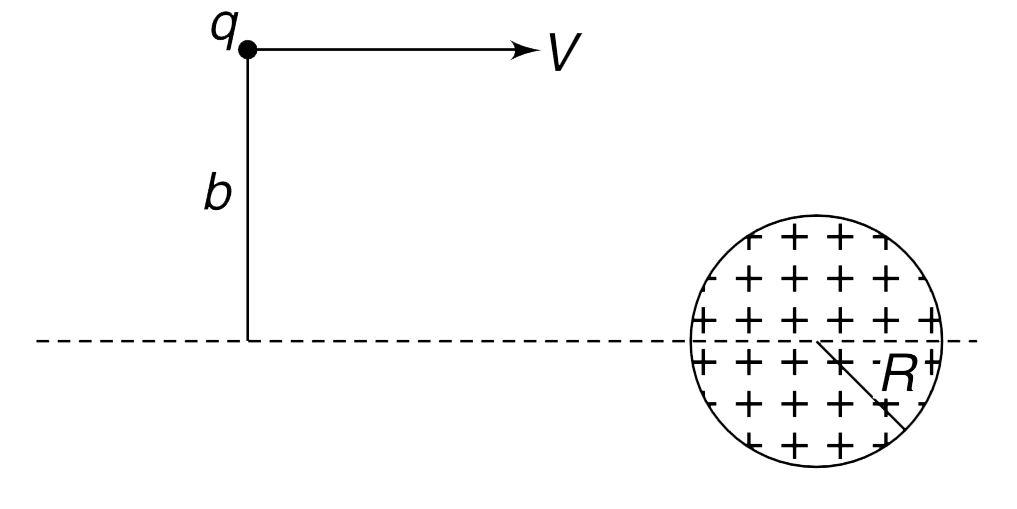
View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
View SolutionA circular coil of 120 turns has a radius of 18cm and carries a current of 3⋅0A. What is the magnitude of the magnetic field (i) at the centre of the coil (ii) at a point on the axis of the coil at a distance from the centre equal to the radius of the coil?
View SolutionA coil of N turns and radius R carries a current I. It is unwound and rewound to make another coil of radius R/2, current remaining the same. Calculate the ratio of magnetic moments of the new coil and the original coil.
View SolutionConsider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by B=0.72μ0NIR approximately.
[Such an arrnagement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils. ]
View SolutionRadius of current carrying coil is 'R'. Then ratio of magnetic fields at the centre of the coil to the axial point, which is R√3 distance away from the centre of the coil :-
View SolutionConsider two parallel co-axial circular coils of equal radius R, and number of turn N, carrying equal currents in the same direction and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B=0.72 (mu_(0)NI)/R , approximately. [Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
View SolutionA coil of N turns and radius R carries a current I. It is unwound and rewound to make another coil of radius R/2, current remaining the same. Calculate the ratio of magnetic moments of the new coil and the original coil.
View Solutionदो समरूप कुण्डलियाँ जिनकी त्रिज्या R है, प्रत्येक में एक ही दिशा में I धारा प्रवाहमान है, उन्हें एक सामान्य अक्ष की और रखकर R दुरी से पृथक रखा गया है।दोनों कुंडलियों के बीच मध्य बिंदु पर
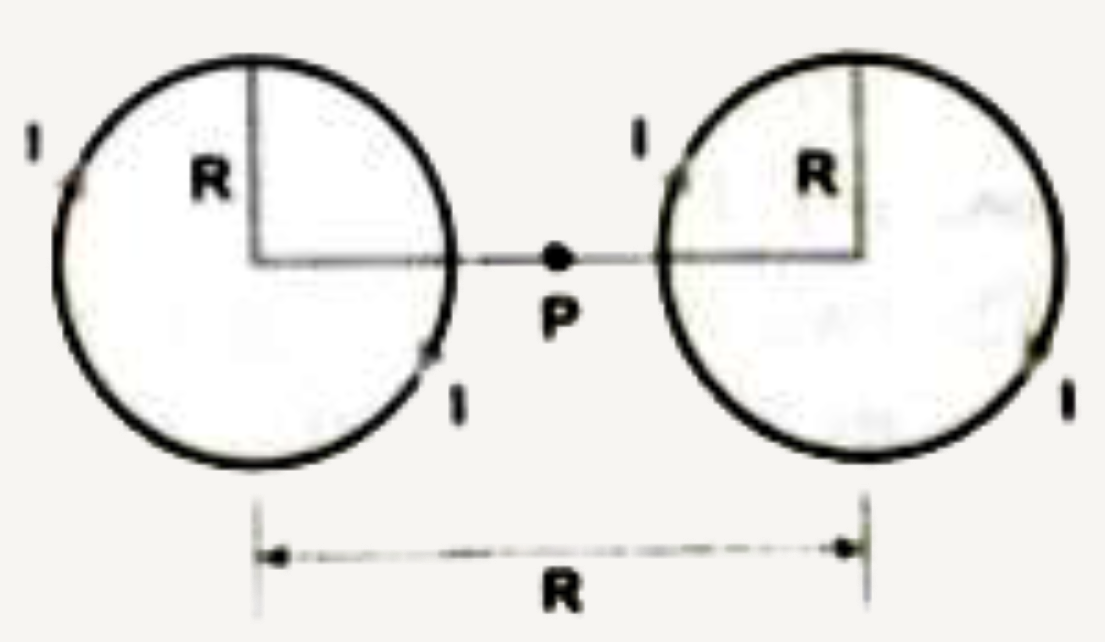
View SolutionTwo identical coils, each with N turns and radius R are Placed coaxially at a distance R as shown in the figure. If I is the current passing through the loops in the same direction, then the magnetic field at a point P which is at exactly at (R )/(2) distance between two coils is ........... .
View SolutionTwo identical coils, each with N turns and radius R are Placed coaxially at a distance R as shown in the figure. If I is the current passing through the loops in the same direction,
then the magnetic field at a point P which is at exactly at R2 distance between two coils is ........... .
View SolutionFor a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B=μ0IR2N2(x2+R2)3/2
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
B=0.72μ0NIR. approximately
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
View SolutionFor a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B=μ0IR2N2(x2+R2)3/2
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
B=0.72μ0NIR. approximately
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
View SolutionFor a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B=μ0IR2N2(x2+R2)3/2
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
B=0.72μ0NIR. approximately
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
View SolutionFor a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B=μ0IR2N2(x2+R2)3/2
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
B=0.72μ0NIR. approximately
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
View Solution
