In the figure shown W1 represent the cross section of an infinitely long wire carrying current I1 into the plane of the fig. AB is a line of length L and the wire W1 is symmetrically located with respect to the line. The line integral ∫BA→B.→dl. d l along the line from A to B is equal to – a0 where a0 is a positive number. Another long wire W2 is placed symmetrically with respect to AB (see fig) and the value of ∫BA→B.→dl becomes zero. Consider a line DC to the right of W2. The line is parallel to AB and has same length. The two wires fall on perpendicular bisector of both lines. If ∫DC→B.→d=2a0 with both wires W1 and W2 present, calculate the ratio of current I2I1 in the two wires.

The correct Answer is:I2I1=1+√2
Topper's Solved these Questions
Similar Questions
A straight current carrying wire has current I directed into the plane of the fig. There is a line AB of length 2a at a distance a from the wire (see fig.). Find the value of line integral ∫BA→B.→dl where →B represents magnetic field at a point due to current I. Will the value of integral change if a is changed? Length of line AB is always double that of a.

View SolutionIn the figure shown a current I1 is established in the long straight wire AB. Another wire CD carrying currrent I2 is placed in the plane of the paper. The line joining the ends of this wire is perpendicular to the wire AB. The resultant force on the wire CD is :
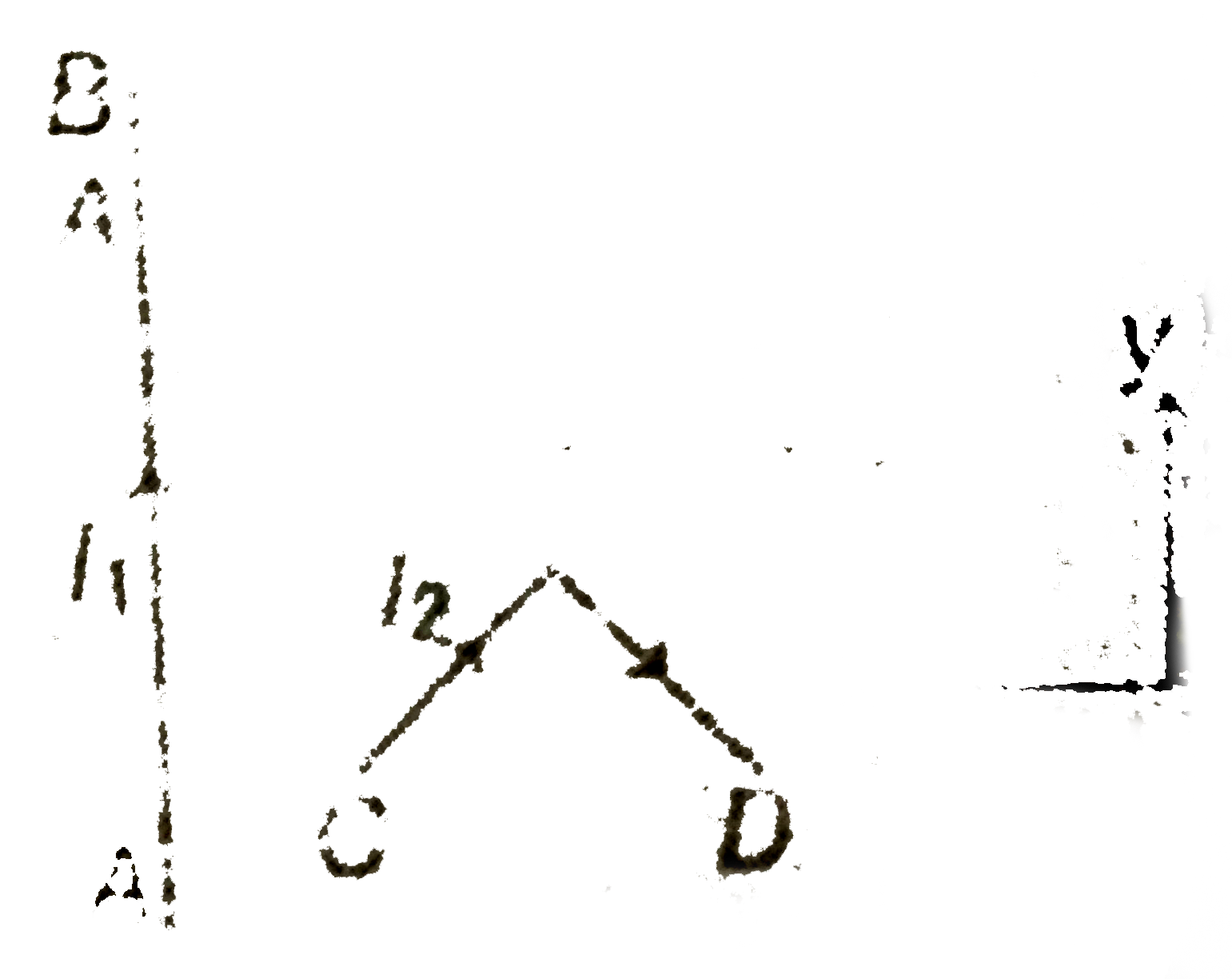
View Solution
Knowledge Check
In the figure shown a current I1 is established in the long straight wire AB. Another wire CD carrying currrent I2 is placed in the plane of the paper. The line joining the ends of this wire is perpendicular to the wire AB. The resultant force on the wire CD is :
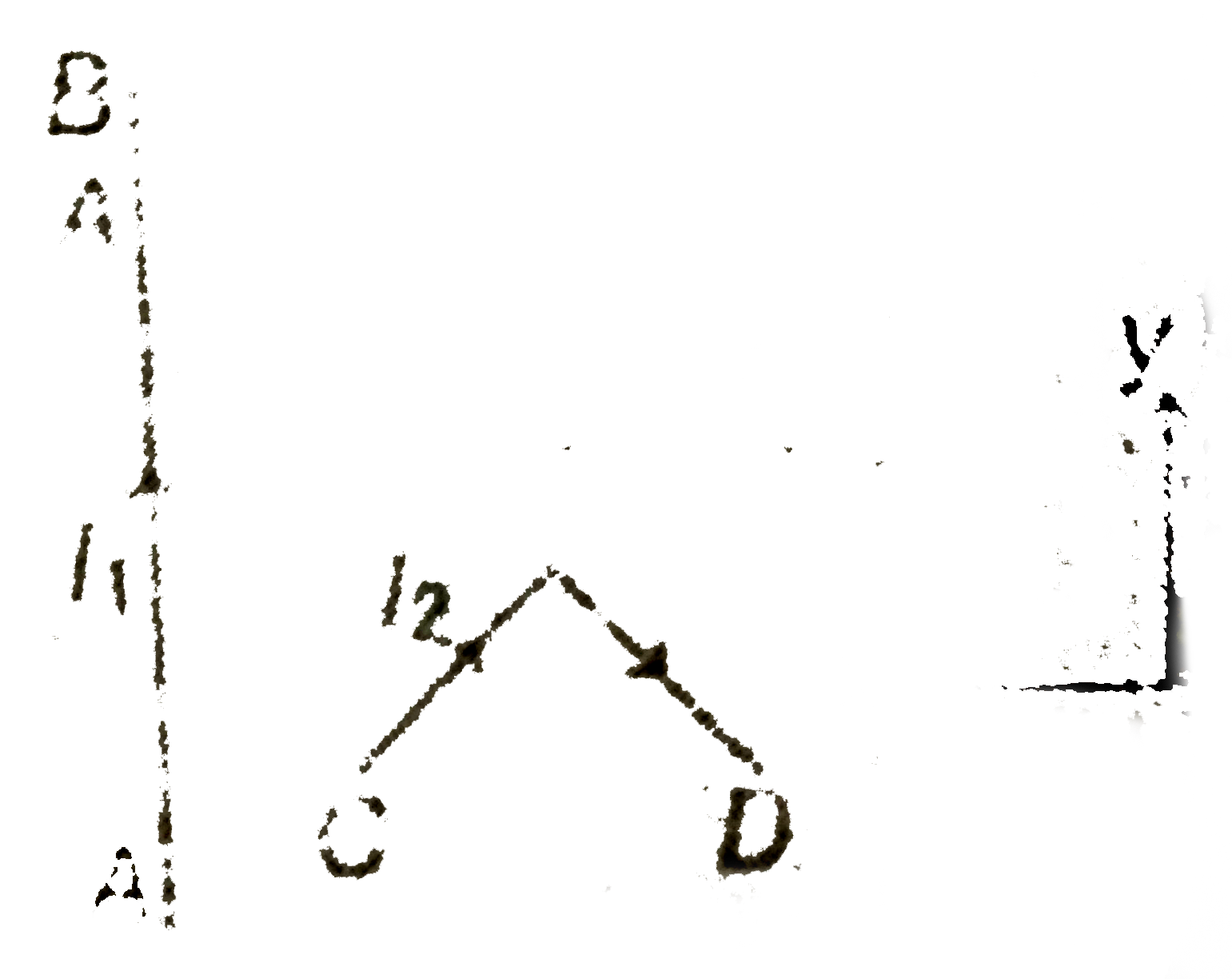 AzeroBtowards negative x-axisCtowards positive y-axisDNone of the above
AzeroBtowards negative x-axisCtowards positive y-axisDNone of the aboveIn the figure shown a current I1 is estabilshed in the log straight wire AB. Another wire CD carrying current I2 is placed in the plane of the paper. The line joining the ends of this wire is perpendicular to the wire AB. The resultant force on the wire CD is:
 AZeroBtowards negative x-axisCtowards positive y-axisDnone of these
AZeroBtowards negative x-axisCtowards positive y-axisDnone of theseA very long cylindrical wire is carrying a current I0 distriuted uniformly over its cross-section area. O is the centre of the cross-section of the wire and the direction of current in into the plane of the figure. The value ∫BA→B.→dl along the path AB (from A to B ) is
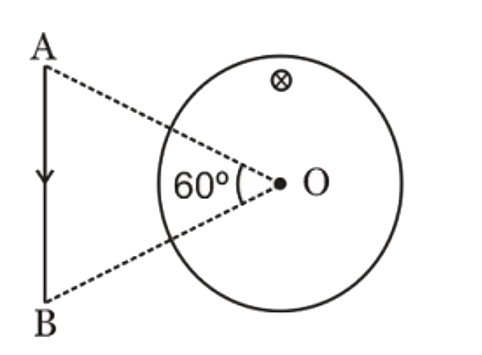 Aμ0I0B−μ0I06Cμ0I06Dμ0I03
Aμ0I0B−μ0I06Cμ0I06Dμ0I03
A very long cylindrical wire is carrying a current I0 distriuted uniformly over its cross-section area. O is the centre of the cross-section of the wire and the direction of current in into the plane of the figure. The value ∫BA→B.→dl along the path AB (from A to B ) is

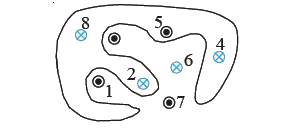
View SolutionEight wires cut the page perpendicularly at the points shown. Each wire carries current i. Odd currents are out of the page and even currents into the page. The line integral ∫→B.→dl-along the loop is
View SolutionAn infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its centre from the wire is d (d>>a). If the loop applies a force F on the wire then :
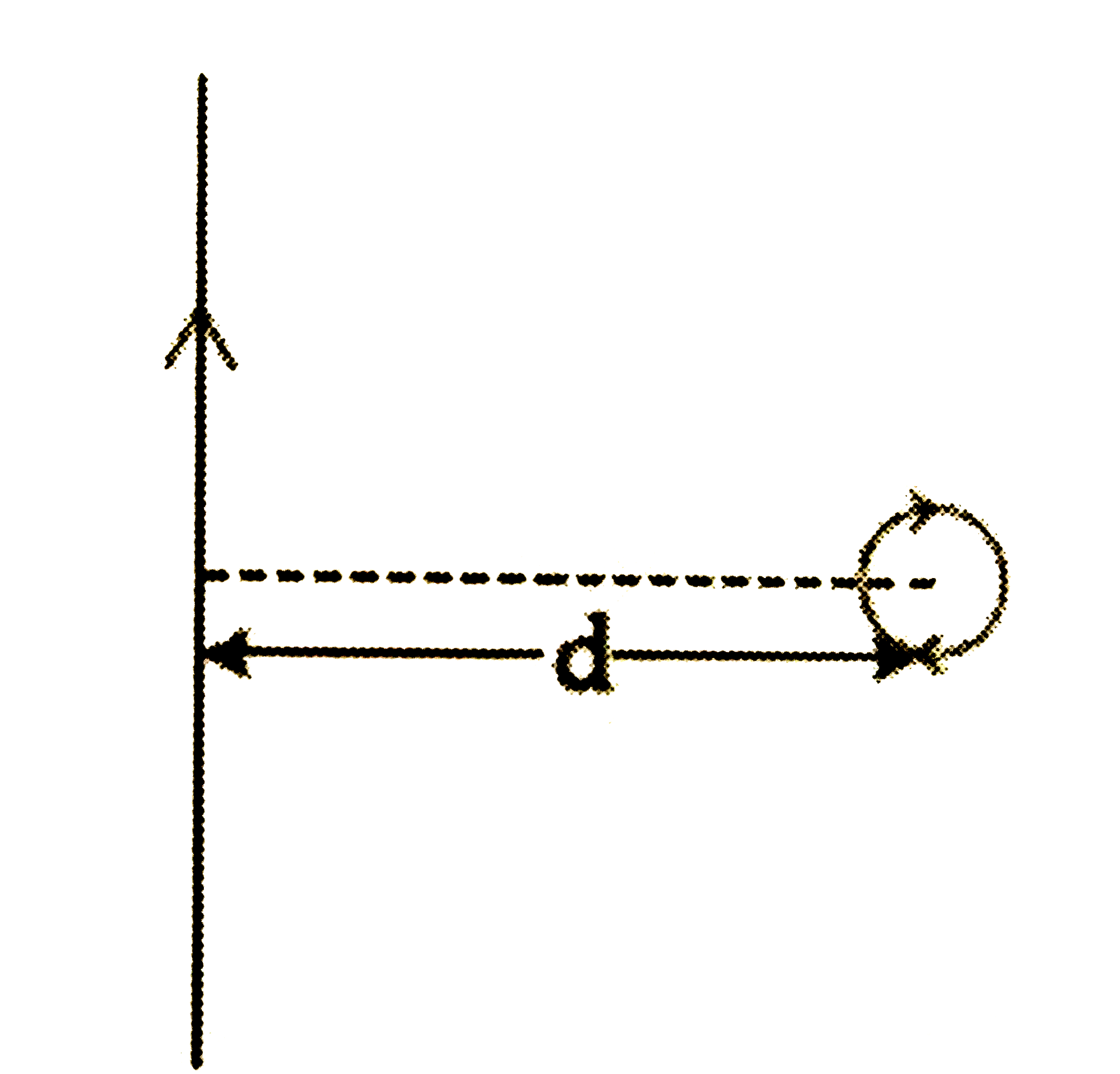
View Solution(a) A long straight wire carries a current I into the plane of the figure. AB is a straight line in the plane of the figure subtending an angle θe point of intersection of the wire with the plane. Find (by integration) the line integral of magnetic field along the line AB.

(b) In the last problem the straight line AB is replaced with a curved line AB as shown in figure. Can you calculate the line integral of magnetic field B along this curved line? If yes, what is its value?

View SolutionEight wires cut the page perpendicularly at the points shown. Each wire carries current i. Odd currents are out of the page and even currents into the page. The line integral ∫→B.→dl-along the loop is

View Solution
