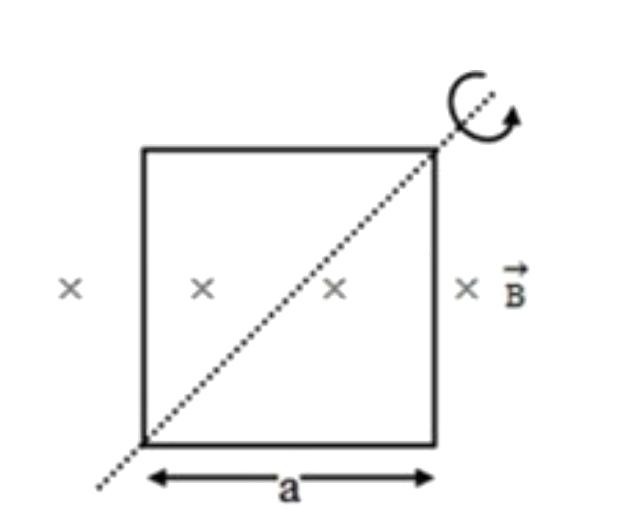
A square loop of mass m and side length a lies in xy plane with its centre at origin. It carries a current I. The loop is free to rotate about x axis. A magnetic field is switched on in the region. Calculate the angular speed acquired by the loop when it has rotated through 90°. Assume no other force on the loop apart from the magnetic force.
The correct Answer is:
Topper's Solved these Questions
Similar Questions
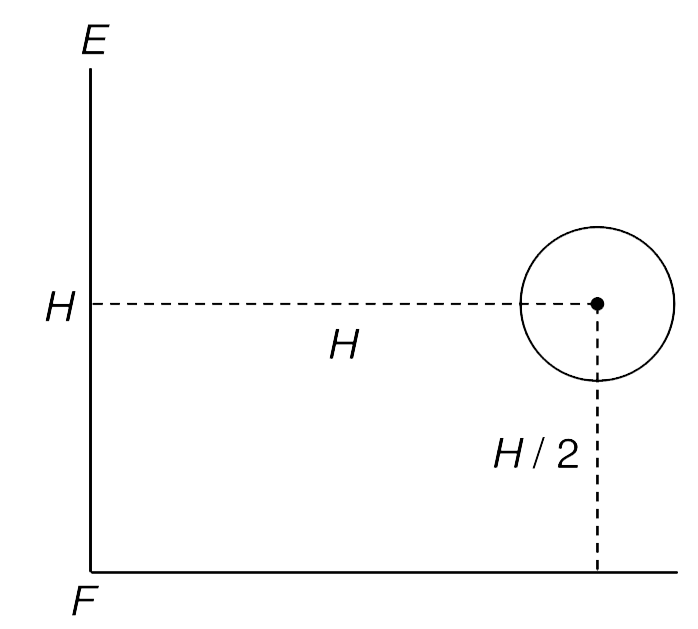
In the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
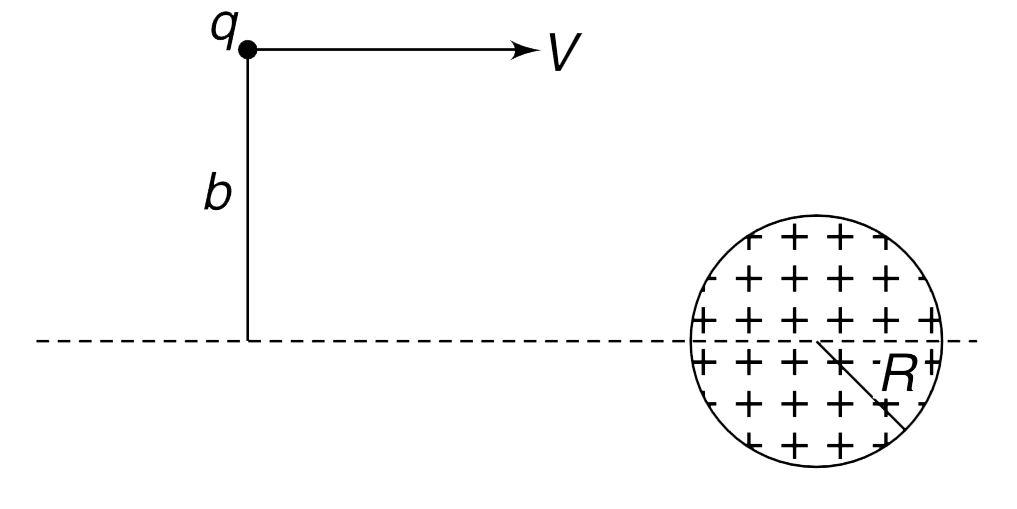
View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA square loop of side a carris a current I . The magnetic field at the centre of the loop is
View SolutionThe magnetic field in a region is given by vec(B)=B_(0)(1+(x)/(a))hat(k) . A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity vec(V)=V_(0)hat(i) . The emf induced in the loop is
View SolutionA square loop of side length L carries a current which produces a magnetic field B0 at the centre (O) of the loop. Now the square loop is folded into two parts with one half being perpendicular to the other (see fig). Calculate the magnitude of magnetic field at the centre O.

View SolutionThe square loop ABCD , carrying a current i , is placed in uniform magnetic field B , as shown. The loop can rotate about the axis XX' . The plane of the loop makes and angle theta(theta lt 90^(@)) with the direction of B . Through what angle will the loop rotate by itself before the torque on it becomes zero
View SolutionA square shaped current loop of side length L and carrying current I lies in a uniform magnetic field B acting perpendicular to the plane of squre loop and directed inward. The net magnetic force acting on current loop is
View SolutionA square loop of length L is placed with its edges parallel to the XY-axies. The loop is carrying the current I. If the magnetic field in the region varies as B=B0(1+xyL2)ˆk, then the magnitude of the force on the loop willl be
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA rigid circular loop of radius r and mass m lies in the XY− plane of a flat table and has a current I flowing in it. At this particular place. The Earth's magnetic field →B=Bxi+Bzk. The value of I so that the loop starts tilting is :
View SolutionA square loop of side b is rotating with angular speed co about one of the diagonals as axis. At t=0, the plane of the loop is perpendicular to the magnetic field B. If the number of turns of the loop be N, then the instantaneous flux through the coil is
View SolutionA conducting circular loop of radiius r carries a constant current i . It is placed in a uniform magnetic field vec(B)_(0) such that vec(B)_(0) is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA rectangular wire loop with side a and b carries current I in the anticlockwise sense and is placed in a uniform magnetic field vec B with its plane perpendicular to vec B . Then the magnetic force on the loop is
View Solution
