In the figure shown the spring constant is K the mass of the upper disc is m and that of the lower disc is 3m the upper block is depressed down from its equilibrium position by a distance δ=5mg/k and released at t=0 find the velocity of m when normal reaction on 3m is mg

zero
g[m/K]1/2
2g[m/K]1/2
4g[m/K]1/2
The correct Answer is:4
N= mg
N+kx=3mg
mg +kx =3 mg
x=2mgk
C.O.E
12k(6mgk)2−12k(2mgk)2−(8mg).kmg
=12mv2
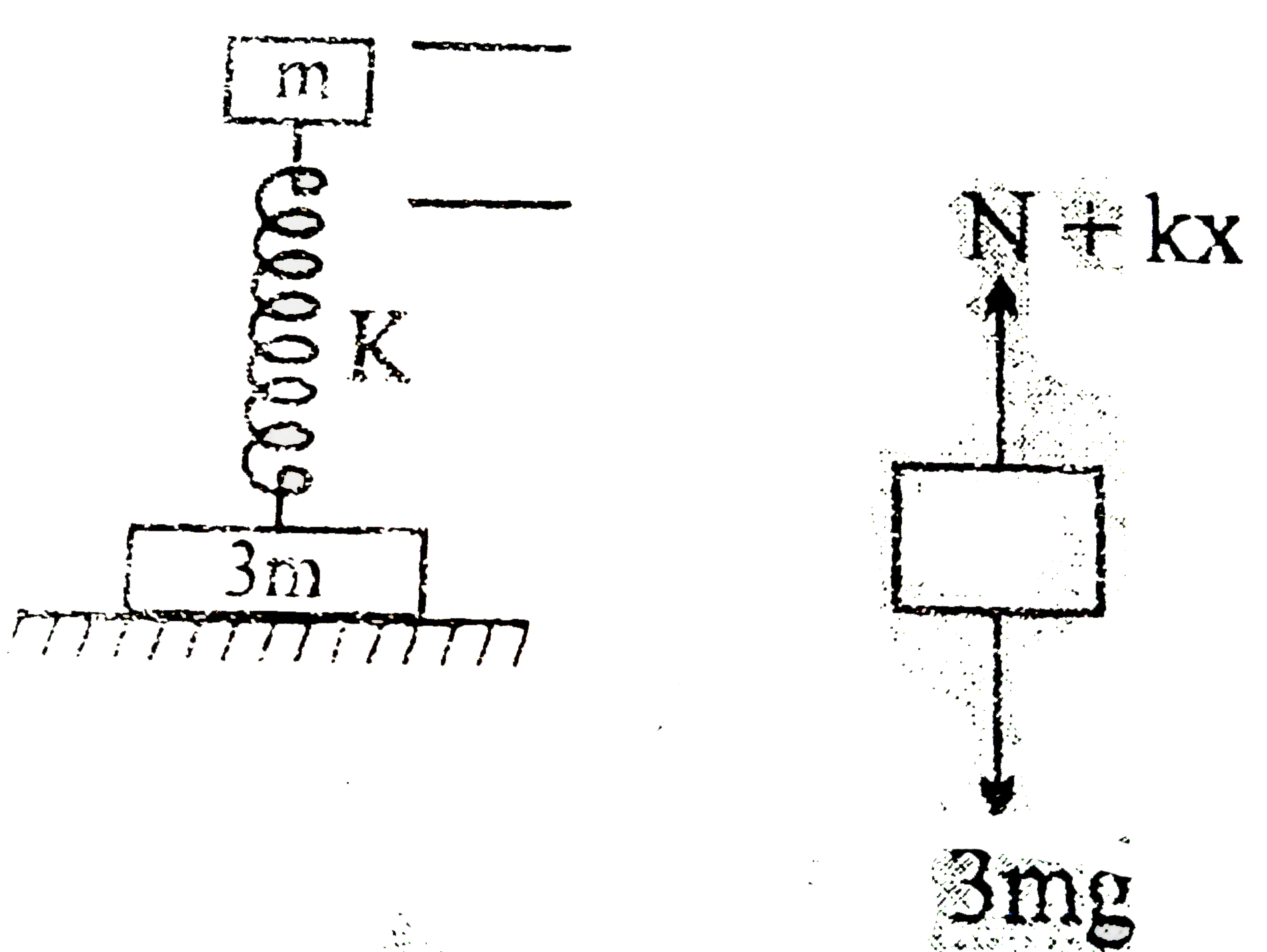
36m2g2k−4m2g2k−16m2g2k=12mv2
16m2g2k=mv2 v=4g[mk]−1/2
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 View Solution
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
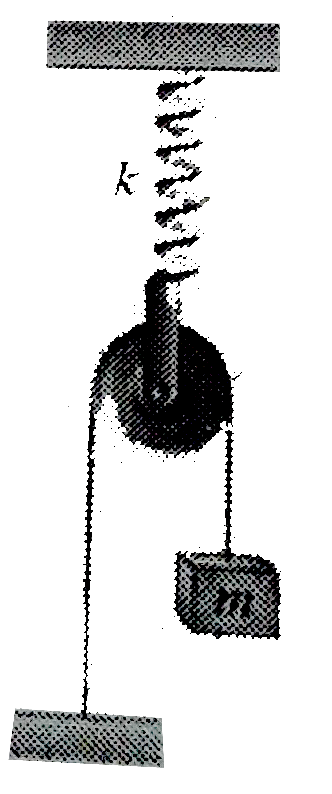 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK - Question 2 - Select One
A block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg/k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg/k
A2B3C4D1 - Question 3 - Select One
An elastic string of constant k is attached to a block of mass m as shown. The block is given an extension of 2mgk from the equilibrium position and released. The time period of oscillations of the block is
 A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
Tow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.
 View Solution
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the amplitude of the oscillation?View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
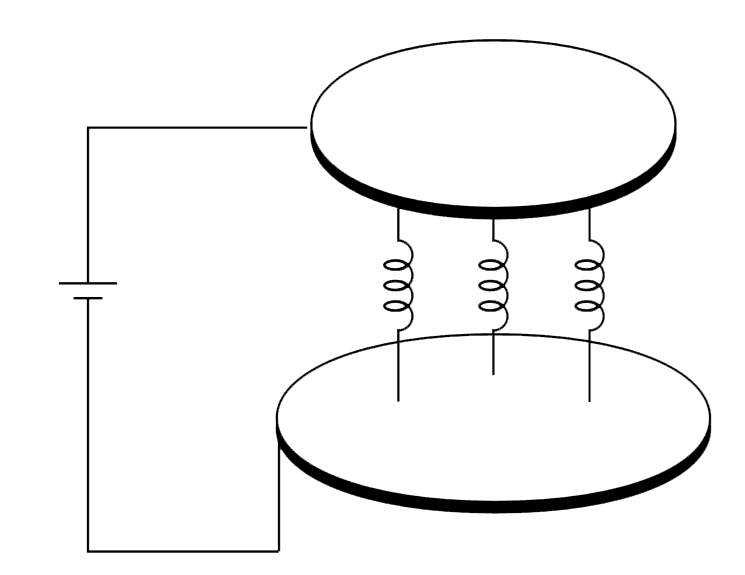
What is the phase constant ϕ for the motion?View SolutionTwo identical metal plates with area A and mass m are kept separated by help of three insulating springs as shown in the Figure. The equilibrium separation between the plates is d0(>>√A) and force constant of each spring is K. When a constant voltage source having emf V is connected to the plates, the equilibrium separation changes to d. Assume that the lower plate is fixed and the upper plate is free to move.
(a) Find V in terms of given parameters.
(b) If the upper disc is slightly displaced from its equilibrium position and released, calculate the time period of its oscillation.
 View Solution
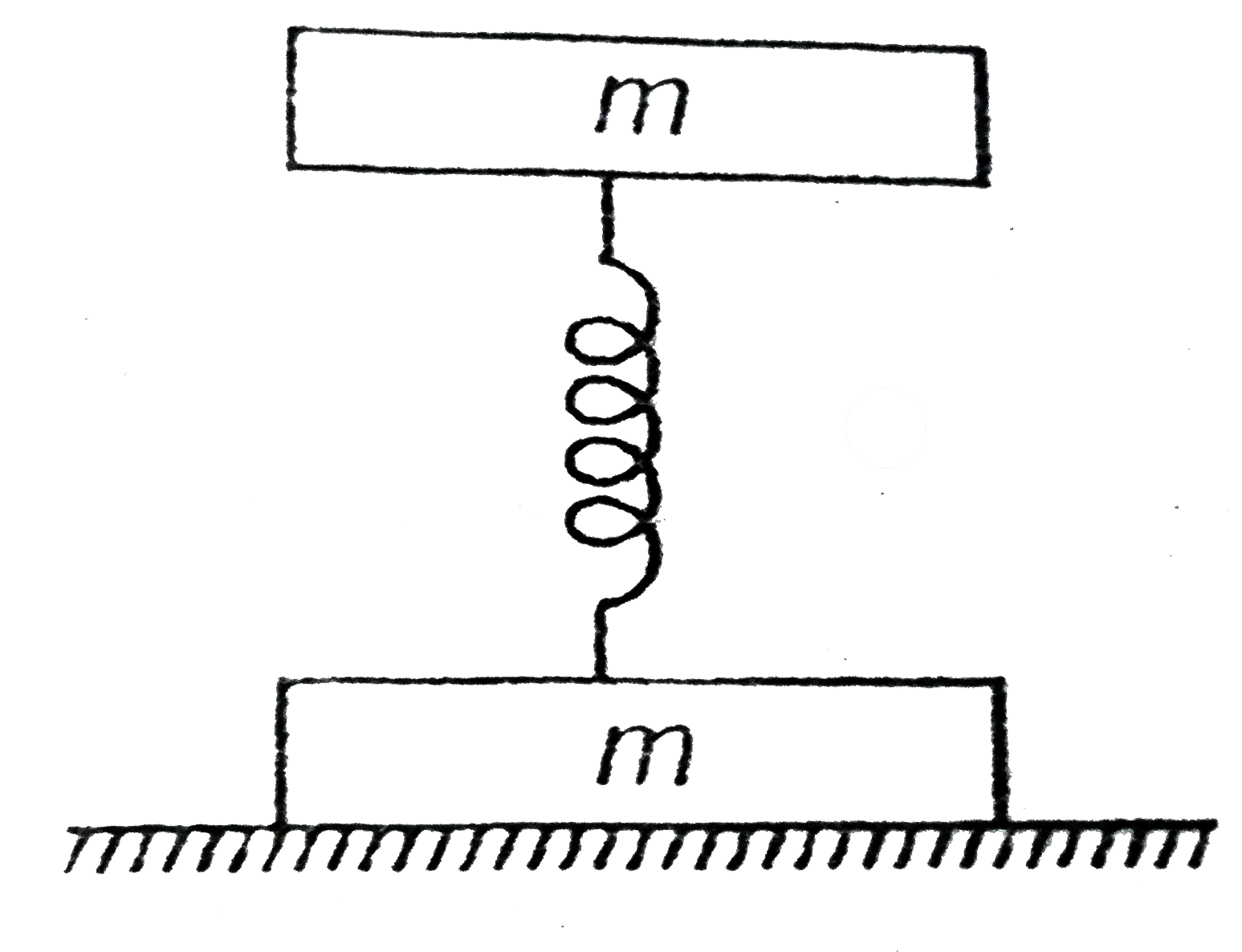
View SolutionFigure shows two discs of same mass m. They are rigidy attached to a spring of stiffness k. The system is in equlibrium. From this equilibrium position, the upper disc is pressed down slowly by a distance x and released. Find the minimum vlue of x, if the lower disc is just lifted off the ground.
 View Solution
View Solution

