A unifrom solid disk of radius R and mass M is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .
.
(23)(gR)1/2
(gR)1/2
(2gR)1/2
2(gR/3)1/2
The correct Answer is:D
Moment of inertia about the axis through the pivot on the rim of the disc is (mR2/2+mR2)=3mR2/2. Using the principle that change in potential energy (mgR) is equal to the gain of kinetic energy (Iω2/2) gives the answer. Also use v=Rω

mgR=12Iω2=12×32mR2ω2
w=√4g3
vc=ωR=√4gR3
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
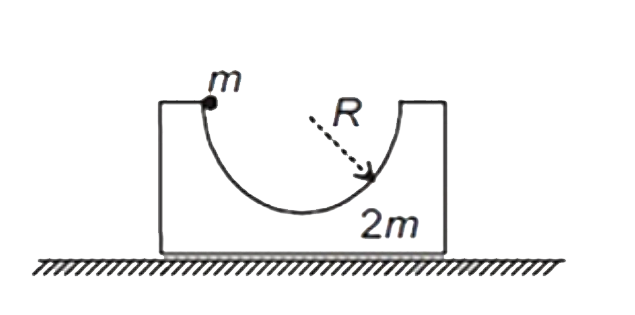
A small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View Solution
Knowledge Check
If the masses are released from the position shown in figure then the speed of mass m1 just before it strikes the floor is -
 A[2m1gd/(m1+m2)]1/2B[2(m1−m2)gd/(m1+m2)]1/2C[2(m1−m2)gd/m1]1/2DNone of the above
A[2m1gd/(m1+m2)]1/2B[2(m1−m2)gd/(m1+m2)]1/2C[2(m1−m2)gd/m1]1/2DNone of the above
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling isA3mg2B2mgCzeroDmg2Three solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
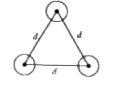 A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
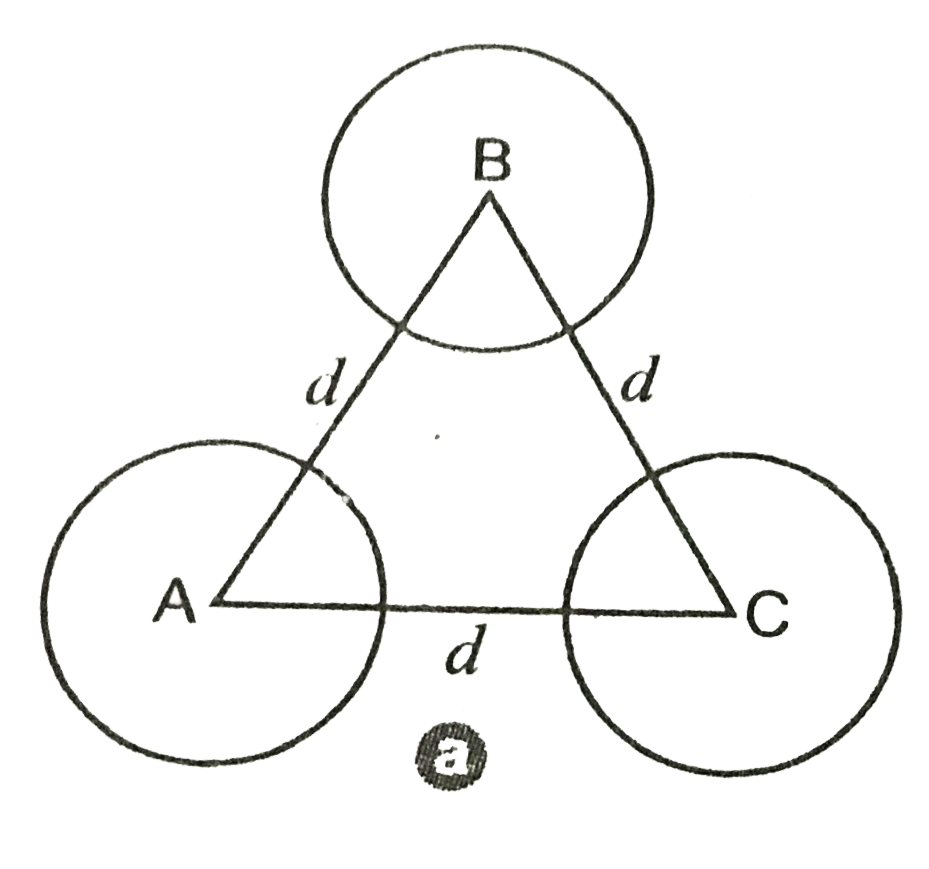
Three solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View SolutionA block of mass m slides along a frictionless surfce as shown in the figure. If it is releases from rest t A what is its speed at B?

View SolutionA uniform slender bar B of mass m and length L supported by a firctionless m and length L supported by a firctionless pivot at A is released from rest at its vertical position as shown the figure. Calculate the reaction at pivot when the bar just acquires the horizontal position shown dotted.

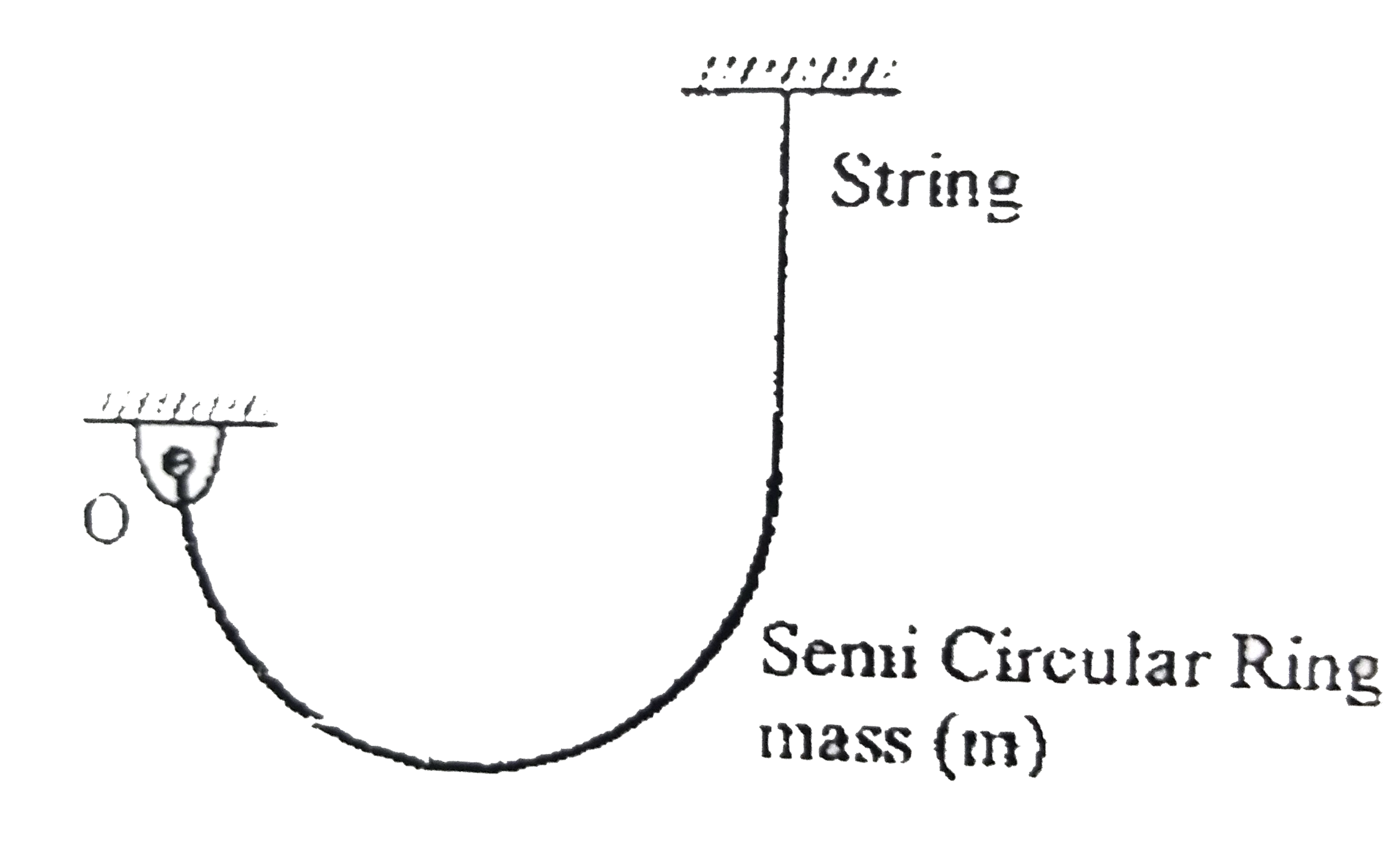
View SolutionThe semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
View SolutionA uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
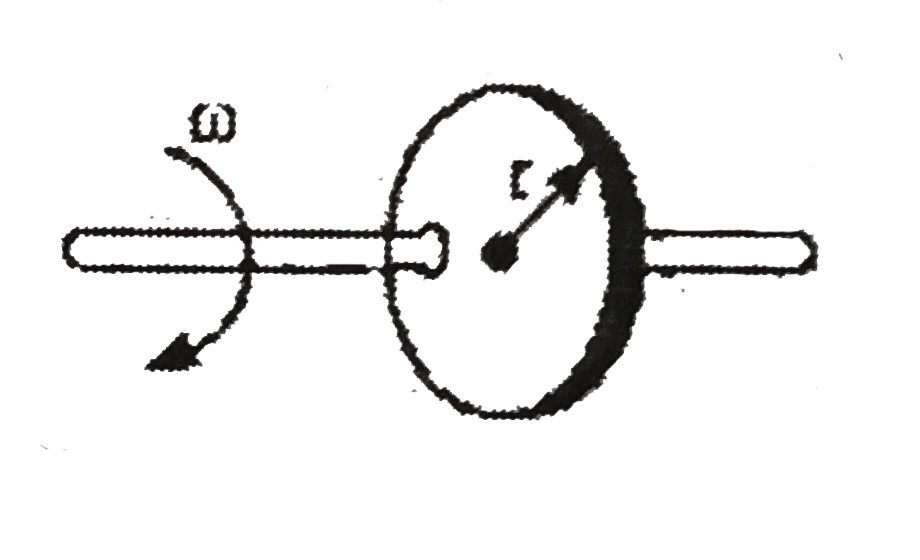
View Solution
