If the system is suspended by the mass m the length of the spring is l1. If it is inverted and hung by mass M, the length of the spring is l2. Find the natural length of the spring.

ml1+Ml2m+M
ml2+Ml1m+M
ml1−Ml2m−M
ml2−Ml1m−M
The correct Answer is:C
k(l1−l0)=Mg
k(l2−l0)=mg
l1−l0l2−l0=Mm
ml1−ml0=Ml2−Ml0
l0=ml1−Ml2m−M
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A massless spring of natural length of 0.5 m and spring constant 50 N/m has one end fixed and the other end attached to a mass of 250 g. The spring mass system is on a smooth floor. The mass is pulled until the length of the spring is 0.6 m and then released from rest. The kinetic energy of the mass when the length of the spring is 0.5 m is
View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block is attached to a spring of stiffness k. The other end of the spring is attached to a fixed wall. The entire system lie on a horizontal surface and the spring is in natural state. The natural length of the springs is l0 if the block is slowly lifted up vertically to a height 512l0 from its initial position :
AThe work done by the lifting force =kl20288+512mgl0BThe work done by the spring force =kl20288CThe work done by the gravity =512mgl0DThe work done by lifting force =−512mgl0+kl20288 - Question 2 - Select One
A mass m is hung on an ideal massless spring another equal mass is connected to the other end of the spring the whole system is at rest at t=0 m is released and the system falls freely under gravity assume that natural length of the spring is L0 its initial stretched length is L and the acceleration due to gravity is g what is distance between masses as function of time
 AL0+(L−L0)cos√2kmtBL0cos√2kmtCL0sin√2kmtDL0+(L−L0)sin√2kmt
AL0+(L−L0)cos√2kmtBL0cos√2kmtCL0sin√2kmtDL0+(L−L0)sin√2kmt
Block of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.
 View Solution
View SolutionA spring with natural length l0 has a tension T1 when its length is l1 and the tension is T2 when its length is l2.The natural length of spring will be:
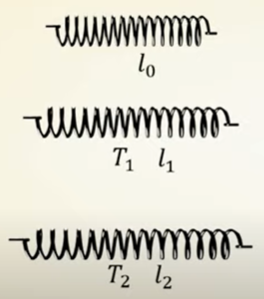 View Solution
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionA particle of mass m is moving with a constant speed v in a circular path in a smooth horizontal plate (plan of the paper ) by a spring force as shown in figure If the natural length of the spring is l0 and stiffeness of the spring is k find the elongation of the spring
 View Solution
View SolutionThe length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
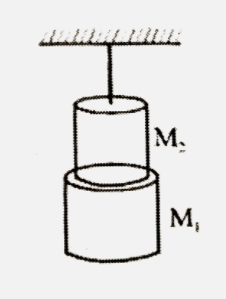 View Solution
View SolutionTwo block-spring mass system are moving on smooth horizontal surface as shown in the figure as t=0. find out the minimum time t when the spring is maximum elongated l0 is the natural length of spring.
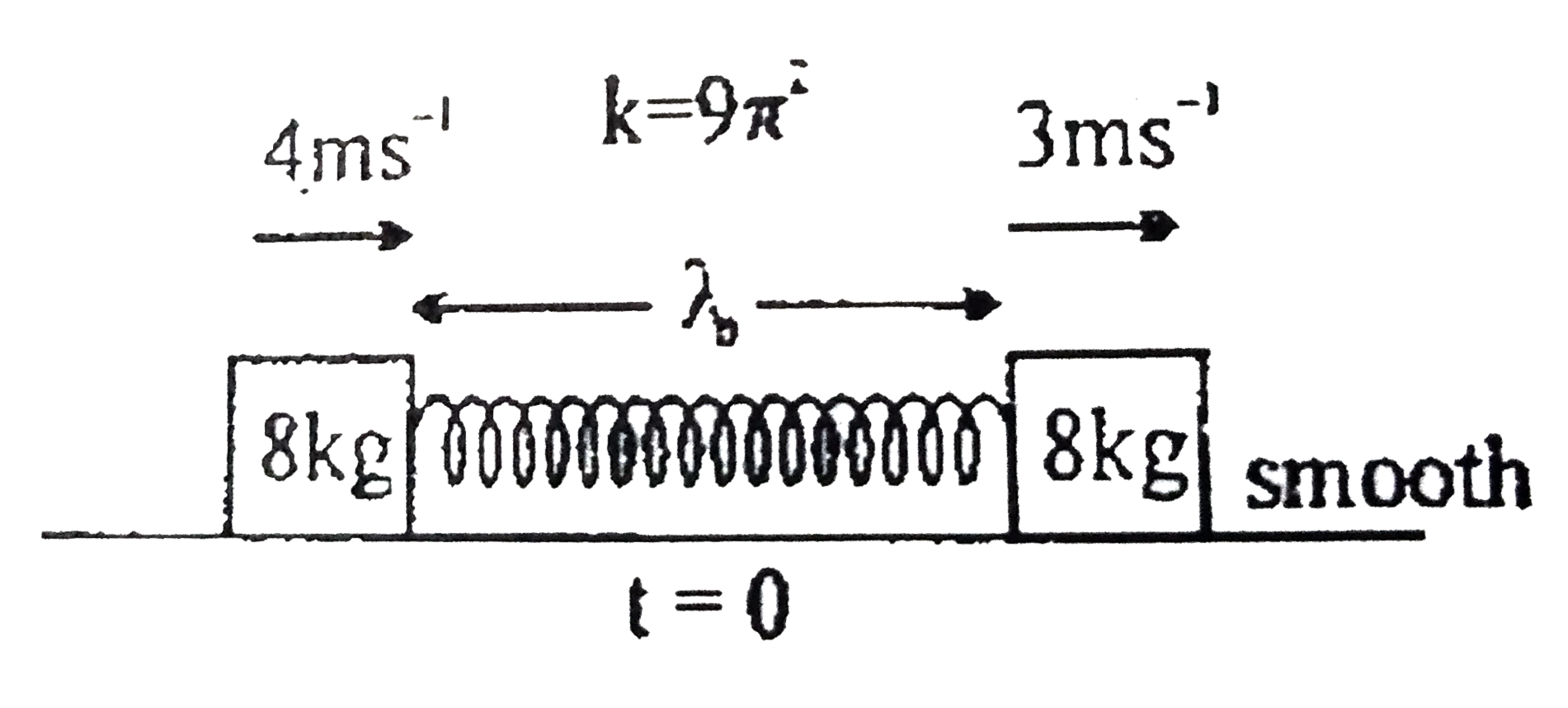 View Solution
View Solution

