Two particles of mass m each are rotating parallel to xz plane in circle of radius R as shown. They are connected by a mass less rod of length $2 \sqrt{2} R$ as shown.

Consider the situation when the particles are at (R, R,0) and (-R, -R, 0). Neglect gravity and any kind of friction. Answer following questions
Choose the correct statement

Text Solution

Verified by Experts

The correct Answer is:C

L in y direction remains constant $z_{y} = 0$

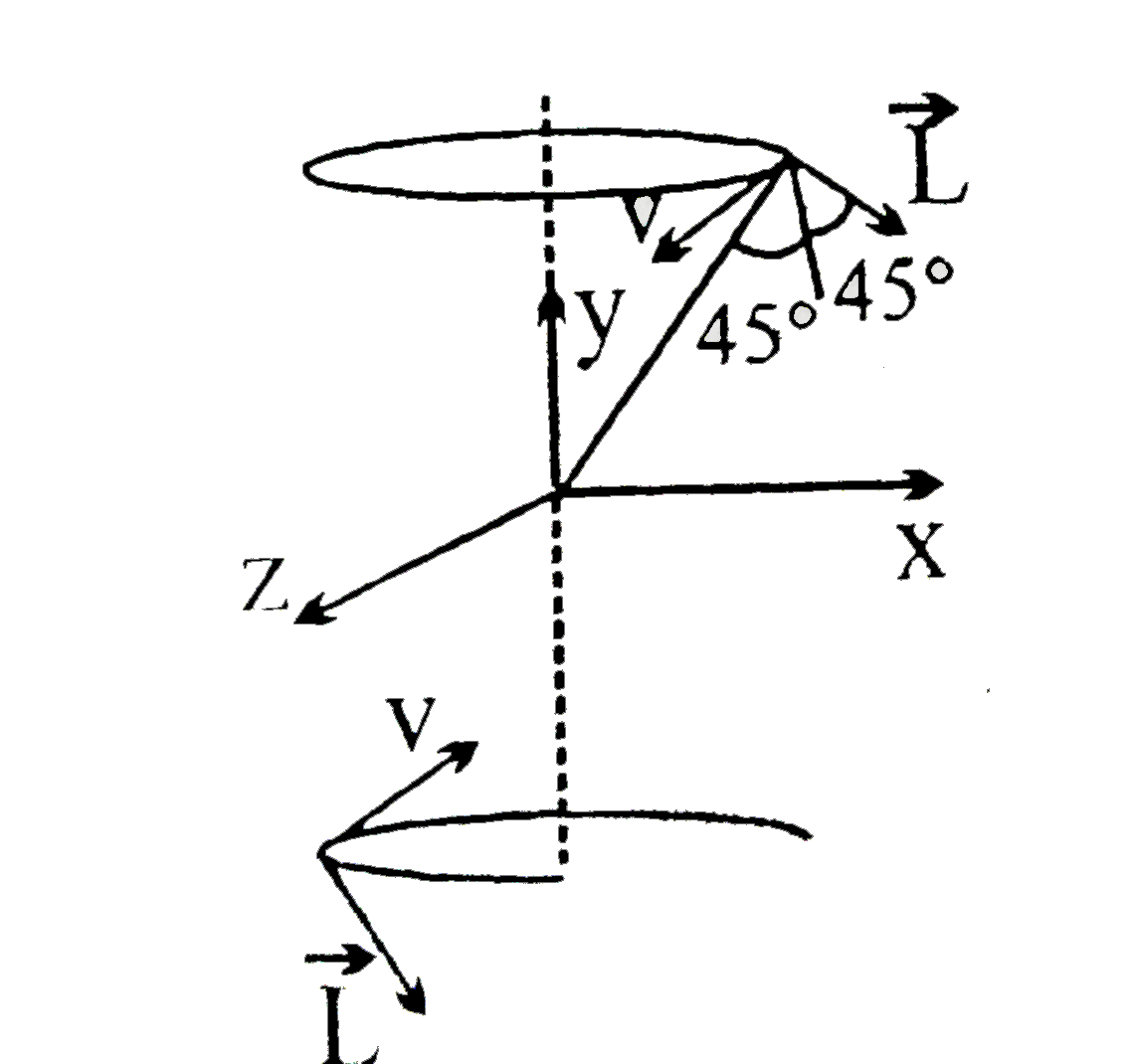
L at this instant is along x direction & rotates in xz plane
$\Rightarrow Δ \to L$ rotates in xz plane

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two particles of mass m each are rotating parallel to xz plane in circle of radius R as shown. They are connected by a mass less rod of length $2 \sqrt{2} R$ as shown.

Consider the situation when the particles are at (R, R,0) and (-R, -R, 0). Neglect gravity and any kind of friction. Answer following questions
The angular velocity vector of the system of two particles and the total angular momentum of system about origin make an angle of
A $45^{\circ}$
B $90^{\circ}$
C $0^{\circ}$
D $180^{\circ}$
Question 2 - Select One
If a particle of mass m is moving in a horizontal circle of radius r with a centripetal force $(- 1 / r^{2})$ , the total energy is
A $- \frac{4}{r}$
B $- \frac{2}{r}$
C $- \frac{1}{r}$
D $- \frac{1}{2 r}$
Question 3 - Select One
A paricle of mass $m$ is tied to a light string of length $L$ and moving in a horizontal circle of radius $r$ with speed $v$ as shown. The forces acting on the particle are

A $m g and T$
B $m g, T, \frac{m v^{2}}{r}$ directed in wards
C $m g, T, \frac{m v^{2}}{r}$ directed outewards
D $\frac{m v^{2}}{r}$ only

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile