In the figure, a solid uniform cube is placed on a horizontal surface. The co-efficient of friction between them is μ where μ<12. A variable horizontal force perpendicular to one edge and passing through the midnight of that applied on the cube's upper face. The maximum acceleration with which it can move without toppling is

μg
g(1−2μ)2
g(1−2μ)
(μ+12)g
The correct Answer is:C

F−μmg=ma
mg×l2+mal2=Fl
mgl2+Fl2−μmg=Fl
F=(1−μ)mg⇒a=(1−2μ)g
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A solid cube is placed on a horizontal surface. The coefficient of friction between them is μ=0.25. A variable horizontal force is applied on the cube’s upper face, perpendicular to one edge and passing through the mid-point of edge, as shown in figure. The maximum acceleration with which it can move without toppling is (take g=10m/s2 )
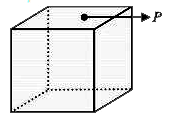 View Solution
View SolutionA uniform rod ABC of mass M is placed vertically on a rough horizontal surface. The coefficient of kinetic friction between the rod and the surface is μ.A force F (>μmg) is applied on the rod at point B at distance l/3 below centre of the rod as shown in figure. The initial acceleration of point A is
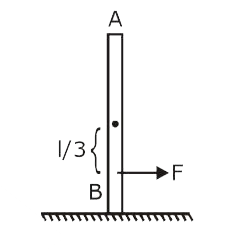 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A block of mass m is placed on a rough horizontal surface. The coefficent of friction between them is μ. An external horizontal force is applied to the block and its magnitude is gradually increased. The force exerted by the block on the surface is R.
AThe magnitude of R gradually increase.BR≤mg√μ2+1.CThe angle made by R with the vertical will gradually increase.DThe angle made by R with the vertical ≤tan−1μ. - Question 2 - Select One
A block of mass m is placed on a horizontal surface. The coefficient of frication between them is μ. The block has to be moved by applying a single external force on it. The force may be applied in my direciton. The minimum value of this force must be
Amg, applied vertically upward, if μ>1Bμmg, applied horizontally, if μ<1Cμmg√μ2+1 for all values of μDμ2mgμ2+1 for all values of μ - Question 3 - Select One
A solid sphere of mass 10kg is placed on a rough surface having coefficient of friction μ=0.1. A constant force F=7N is applied along a line passing through the centre of the sphere as shown in the figure. The value of frictional force on the sphere is.
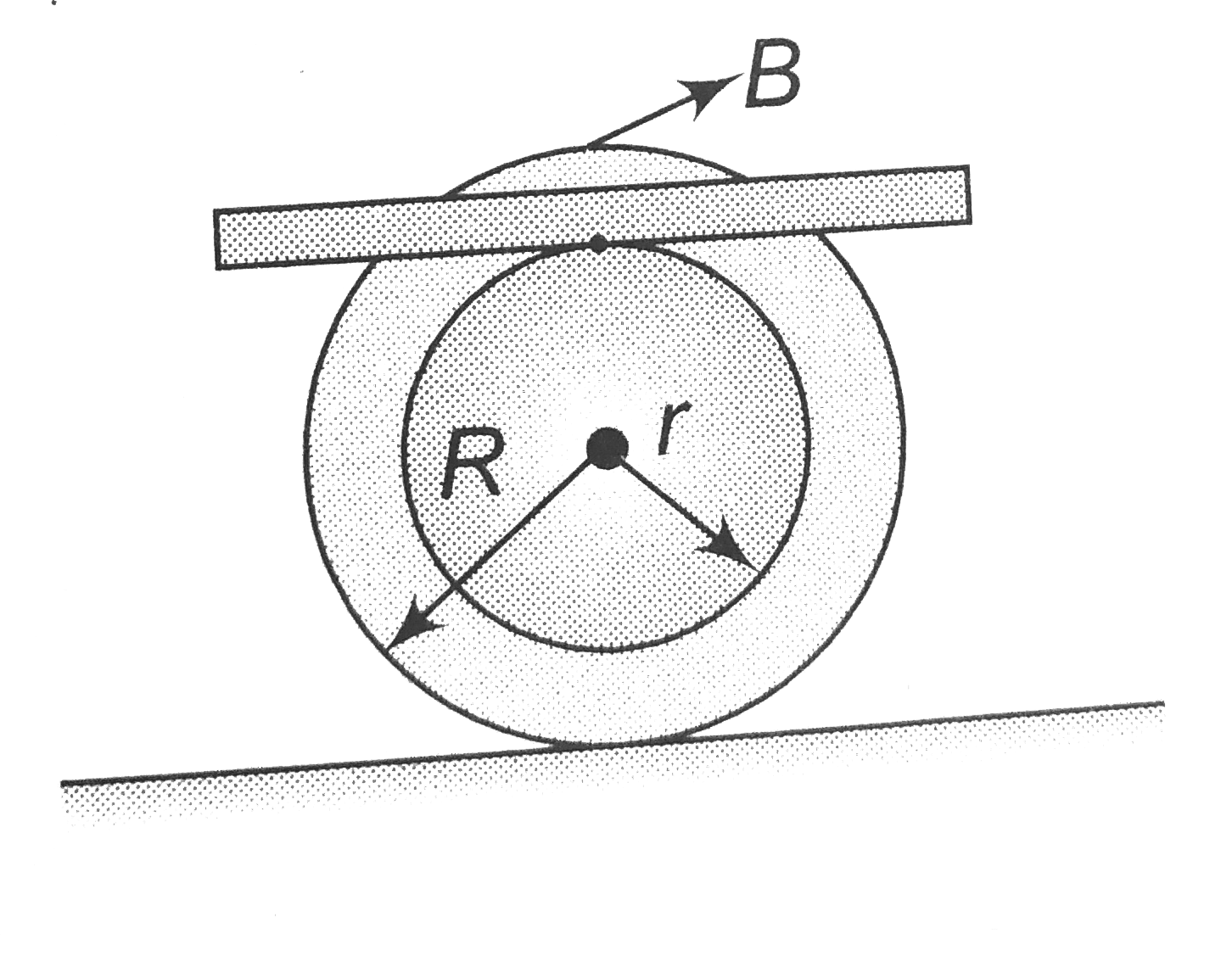 .A1 NB2 NC3 ND7 N
.A1 NB2 NC3 ND7 N
A block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)
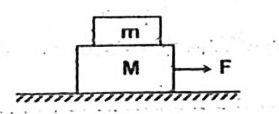 View Solution
View Solution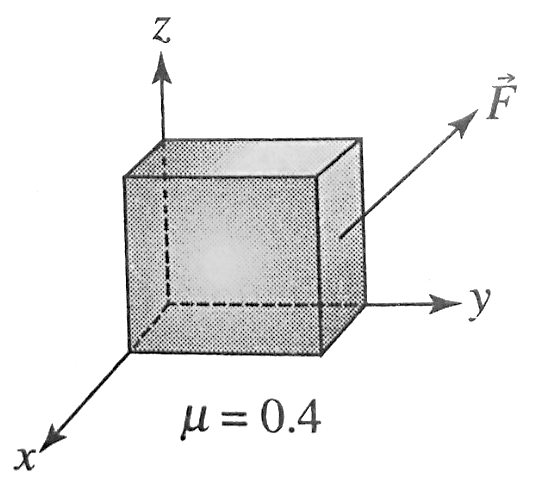
A solid cube of mass 5 kg is placed on a rough horizontal surface, in xy-plane as shown. The friction coefficient between the surface and the cube is 0.4. An external force →F=6ˆi+8ˆj+20ˆkN is applied on the cube. (use g=10ms2)View SolutionA solid cube of mass 2kg is placed on rough horizontal surface, in xy−plane as shown. The friction coefficient between the surface and the cube is 0.2. An external force 3ˆi+4ˆj+5ˆkN is applied on the cube. (use g=10m/s2)
 View Solution
View SolutionTwo block A and B of masses 6kg and 3kg rest on a smooth horizontal surface as shown in figure If coefficient of friction between A and Bb is 0.4 the maximum horizontal force which can make them move without separation is
 View Solution
View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?
 View Solution
View Solution

