The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The maximum speed of junction P is $V_{0}$ . Assume springs are massless. Select the correct option/s

A

Amplitude of potential energy is springs $S_{1}$ and $S_{2}$ is respectivley $\frac{1}{9} k A^{2}$ and $k A^{2}$

B

Amplitude of potential energy is $S_{1}$ and $S_{2}$ is respectively $\frac{2}{9} k A^{2}$ and $\frac{1}{9} k A^{2}$

C

$V_{0} = A \sqrt{\frac{8 k}{27 M}}$

D

$V_{0} = A \sqrt{\frac{8 k}{81 M}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:BC

$\frac{2 k}{3} A = k S_{p}$
$S p_{1} = \frac{2}{3} A$
$S p_{2} = \frac{A}{3}$
$U_{1 max} = \frac{1}{2} k \times \frac{4 A^{2}}{9} = \frac{2 k A^{2}}{9}$
$U_{2 max} = \frac{1}{2} 2 k \times \frac{A^{2}}{9} = \frac{k A^{2}}{9}$
$V_{0} = \frac{2 A}{3} \times \sqrt{\frac{2 k}{3 m}}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is

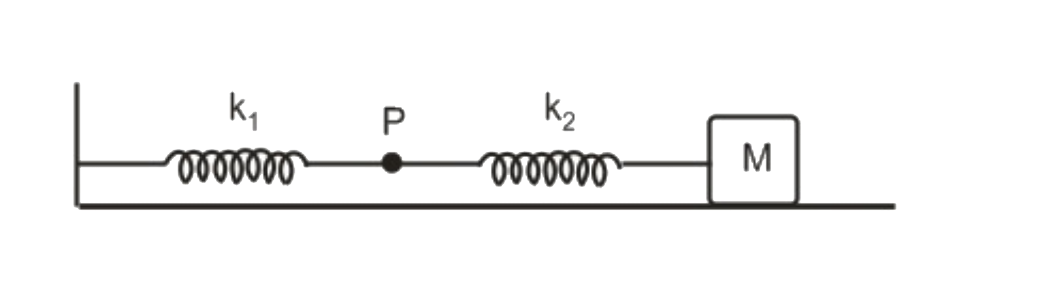A $\frac{k_{1} A}{k_{2}}$
B $\frac{k_{2} A}{k_{2} - k_{1}}$
C $\frac{k_{2} A}{k_{1} + k_{2}}$
D $\frac{k_{2} A}{k_{1}}$
Question 2 - Select One
The mass $M$ shown in the figure oscillates in simple harmnonic motion and amplitude $A$ . The amplitude of the point $P$ is

A $\frac{k_{1} A}{k_{2}}$
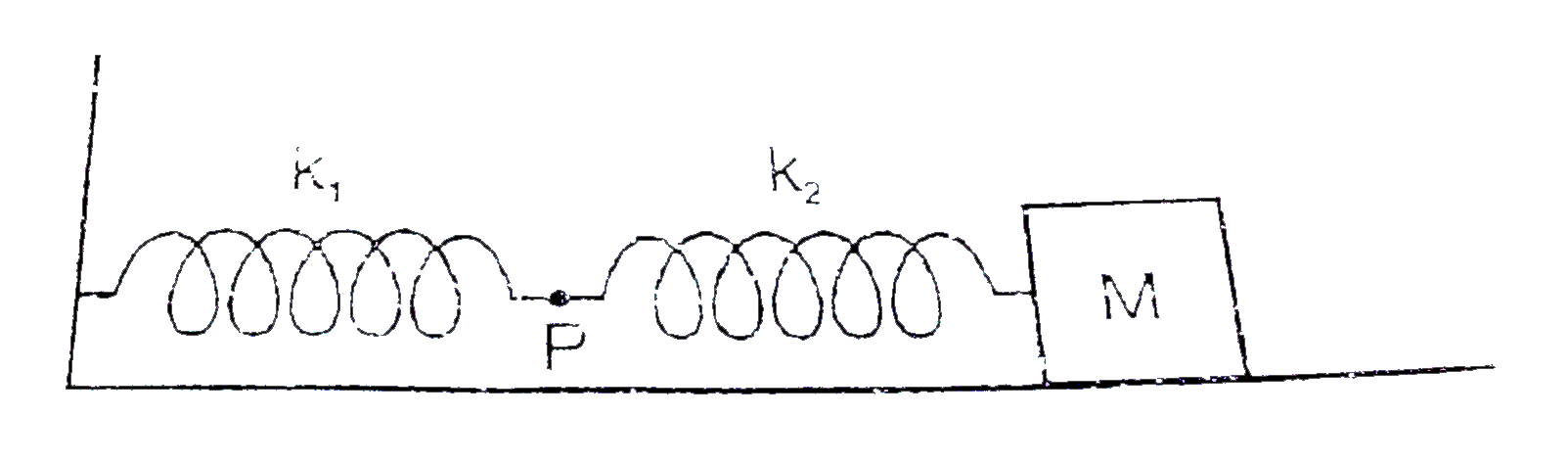B $\frac{k_{2} A}{k_{1}}$
C $\frac{k_{1} A}{k_{1} + k_{2}}$
D $\frac{k_{2} A}{k_{1} + k_{2}}$
Question 3 - Select One
For a particle executing simple harmonic motion, the amplitude is A and time period is T. The maximum speed will be
A4AT
B $\frac{2 A}{T}$
C $2 π \sqrt{\frac{A}{T}}$
D $\frac{2 π A}{T}$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile