Two bodies of masses 2 kg and 3 kg are connected by a metal wire of cross-section 0.04 mm2 and are placed on a frictionless horizontal surface. Breaking stress of metal wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is
100 N
150 N
200 N
250 N
The correct Answer is:D
To solve the problem, we need to determine the maximum force F that can be applied to the 3 kg block without breaking the metal wire connecting it to the 2 kg block.
1. Identify the Given Data:
- Mass of block 1, m1=2kg
- Mass of block 2, m2=3kg
- Cross-sectional area of the wire, A=0.04mm2=0.04×10−6m2=4×10−8m2
- Breaking stress of the wire, σ=2.5GPa=2.5×109Pa
2. Calculate the Maximum Tension (T) in the Wire:
- The maximum tension in the wire can be calculated using the formula for stress:
σ=TA
- Rearranging for T:
T=σ×A
- Substituting the values:
T=(2.5×109Pa)×(4×10−8m2)=100N
3. Relate Tension to the Applied Force (F):
- When a force F is applied to the 3 kg block, both blocks will accelerate together. The acceleration a can be expressed as:
a=Fm1+m2=F2+3=F5
- The tension in the wire (which is the force acting on the 2 kg block) can be expressed as:
T=m1⋅a=2⋅a=2⋅F5=2F5
4. Set the Tension Equal to the Maximum Tension:
- Since the maximum tension T we calculated is 100 N, we set up the equation:
2F5=100
5. Solve for the Maximum Force (F):
- Rearranging the equation gives:
2F=100×5
2F=500
F=5002=250N
Final Answer:
The maximum force F that can be applied to the 3 kg block without breaking the wire is 250 N.
- Mass of block 1, m1=2kg
- Mass of block 2, m2=3kg
- Cross-sectional area of the wire, A=0.04mm2=0.04×10−6m2=4×10−8m2
- Breaking stress of the wire, σ=2.5GPa=2.5×109Pa
- The maximum tension in the wire can be calculated using the formula for stress:
σ=TA
- Rearranging for T:
T=σ×A
- Substituting the values:
T=(2.5×109Pa)×(4×10−8m2)=100N
- When a force F is applied to the 3 kg block, both blocks will accelerate together. The acceleration a can be expressed as:
a=Fm1+m2=F2+3=F5
- The tension in the wire (which is the force acting on the 2 kg block) can be expressed as:
T=m1⋅a=2⋅a=2⋅F5=2F5
- Since the maximum tension T we calculated is 100 N, we set up the equation:
2F5=100
- Rearranging the equation gives:
2F=100×5
2F=500
F=5002=250N
The maximum force F that can be applied to the 3 kg block without breaking the wire is 250 N.
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A 20kg" load is suspended by a wire of cross section 0.4mm^(2).The stress produced in N/m ' is
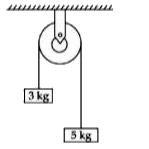
View SolutionTwo blocks of masses 3 kg and 5 kg are connected by a metal wire going over a smooth pulley. The breaking stress of the metal is 24π×102Nm−2 . What is the minimum radius of the wire ?
(take g=10ms−2)
View Solution
Knowledge Check
Two bodies of masses 2kg and 3kg are connected by a metel wire of cross section 0.04 mm2. Breaking stress of metel wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is :
 A100NB150NC200ND250N
A100NB150NC200ND250NA 20kgload is suspended by a wire of cross section 0.4mm2. The stress produced in N/m2 is
A4.9×10−6B4.9×108C49×108D2.45×10−6Three blocks of masses 2 kg , 3 kg and 5 kg are connected to each other with light string and are then placed on a frictionless surface as shown in the figure. The system is pulled by a force F=10Nthen tension T1=
 A1NB5 NC8 ND10 N
A1NB5 NC8 ND10 N
Two blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109m−2. What should be the minmum radius of the wire used if it is not to break? Take g=10ms−2
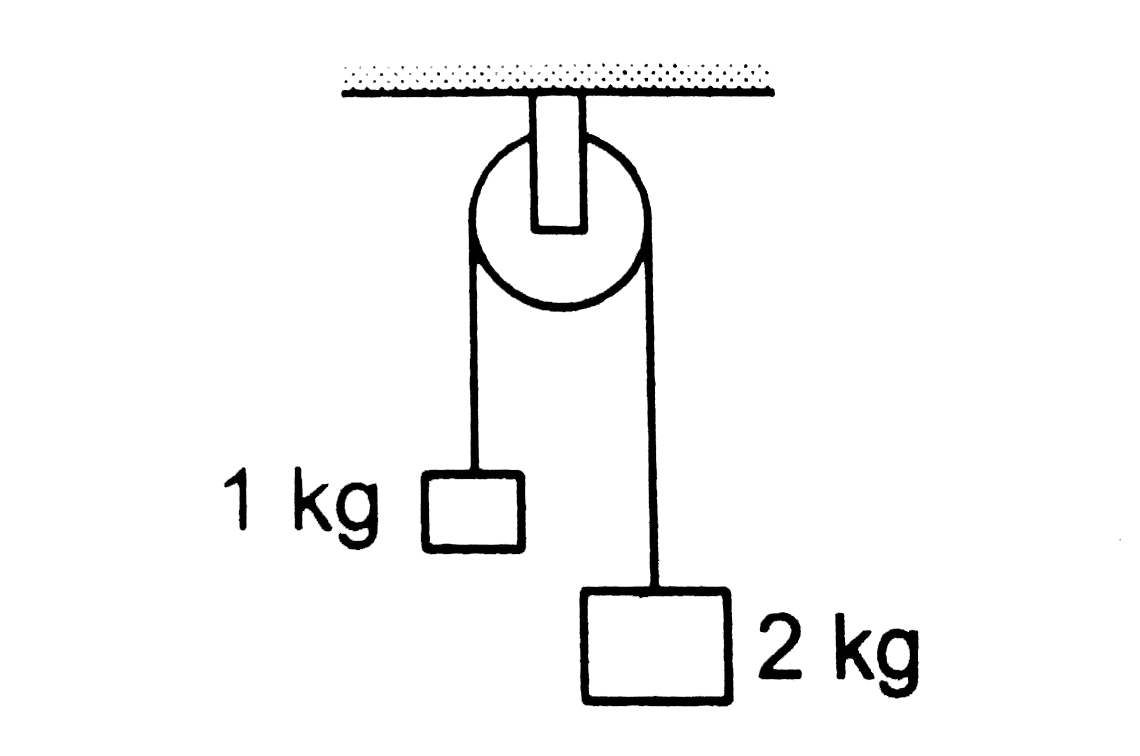
View SolutionTwo bodies of masses 3kg and 2kg are connected by a spring balance Two forces of 10N and 5N are applied on the blocks as shown The reading of the spring balance (in newton) would be
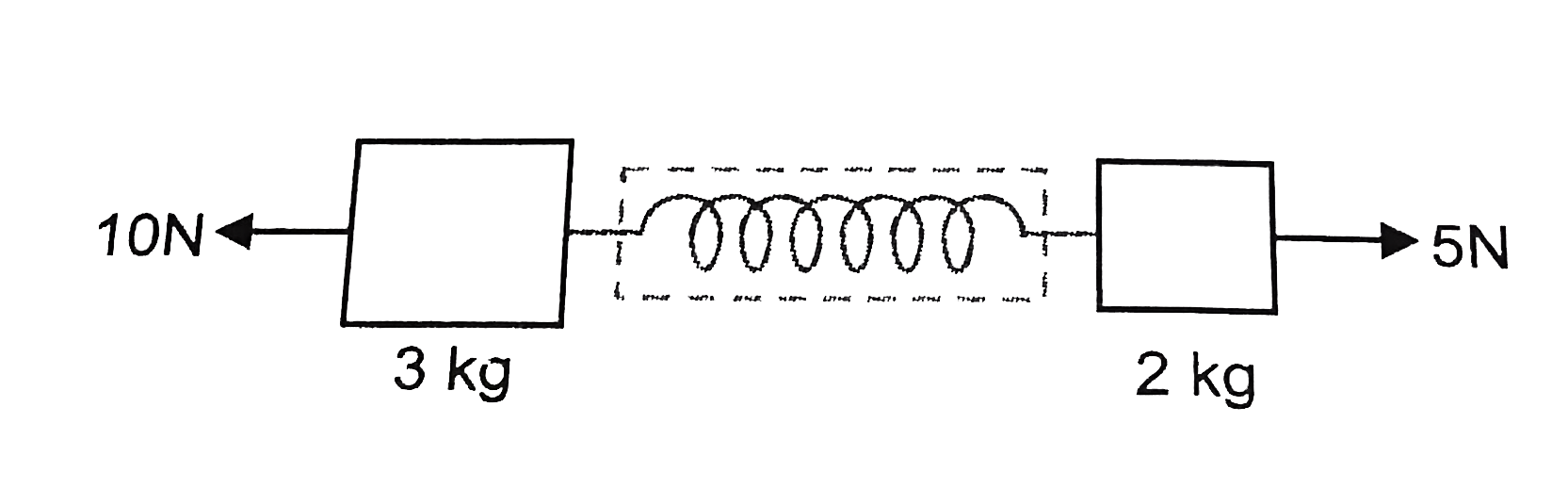 .
.
View SolutionTwo blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is

View SolutionTwo blocks of masses 4 kg and 2 kg are connected by a string. The arrangement is placed on a rough horizontal surface as shown in figure. A time varying force F = 2t. Newton is applied to 2 kg block. The variation of friction force (f2) on the 4 kg block, as a function of time, is represented by the graph :

View SolutionTwo blocks of masses 40 kg and 20 kg are connected by a wire that has a linear mass density of 1g/m. These blocks are being pulled across horizontal frictionless floor by horizontal force F that is applied to 20 kg block. A transverse wave travels on the wave between the blocks with a speed of 400m/s (relative to the wire). the lmass of the wire is negligible compared to the mass of the blocks. the magnitude of F is
View Solution
