Area of a triangle
Area of Triangle
Formula to Find Area of Triangle
There are several ways to determine the area of a triangle. For instance, there is the basic formula that the area of a triangle is a half of the base times the height. This formula just works when the height of the triangle is provided.
Another formula to determine area of triangle is Heron's formula which gives the area in terms of the three sides of the triangle, as the square base of the item s(s – a)(s – b)(s – c) where s is the semiperimeter of the triangle, that is, s = (a + b + c)/2.
Here, we'll consider an equation for the area of a triangle when you have different sides and the included edge of the triangle. If we are provided with the values of the different sides an and b of the triangle, and the included edge C.
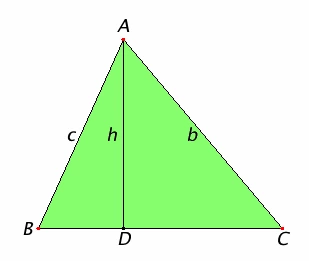
Given Base and Height
If the base of the triangle and the altitude is provided, then we can use the formula.
A= 1/2 x base x height
A= 1/2 x b x h
Area of a triangle is equivalent to half of the product of its base and height.
The height of a triangle is the opposite distance from a vertex to the base .

Any of the 3 sides of a triangle can be considered as a base. Everything depends on where the height is drawn.
Solved Examples of Area of Triangle
Ex 1: Find the area of a triangle with a base of 14 cm and a height of 5 cm.
Sol:
A = (½)× b × h sq.units
⇒ A = (½) × (14 cm) × (5 cm)
⇒ A = (½) × (70 cm2)
⇒ Area of triangle = 35 cm2
Ex 2: Find the area of a triangle with a height of 6cm and a base of 9cm
Sol:
A = (½) × b × h sq.units
⇒ A = (½) × (9 cm) × (6 cm)
⇒ A = (½) × (42 cm2)
⇒ Area of triangle = 21 cm2
Ex 3: Find the area of an obtuse-angled triangle with a height 9cm and a base of 3cm.
Sol:
Area of triangle = (½) × b × h sq.units
⇒ A = (½) × (3 cm) × (9 cm)
⇒ A = (½) × (27 cm2)
⇒ A = 13.5 cm2
Ex 4: The base of a triangle is 4 cm smaller than its perpendicular height. The triangle is 96 cm2. Determine the length of the base.
Sol:
Area = 96cm2.
Base (B) – Height (H) = 4.
Also, 1/2 Base . Height = 96 cm2
∴ H (H – 4) = 192
⇒ Height = 16 cm and Base length = 12 cm
Ex 5: The length of three sides of a scalene triangle are 5cm, 6cm and 7cm, and find the area of the triangle.
Sol: Three sides of the triangle are 5 m, 6 m and 7 m.
∴semi-perimeter = (5 + 6 + 7)/2 = 9cm.
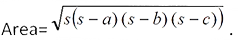
Putting the values in the formula,
Area of triangle = 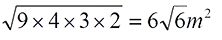
Ex 6: The perimeter of an isosceles triangle is 100 cm. If the length of the base is 30 cm, find the length of the equal sides.
Sol :
Considering the length of equal side = x.
∴ x + x + 30 = 100 cm
⇒ 2x = 70
⇒ x = 35cm.
The length of the equal sides is 35 cm.
Ex 7: A triangle has an area of 625 cm2. One of its sides is given as 125 cm, and then determine the length of the altitude that is dropped on that particular side from the opposite vertex.
Sol: Area of triangle (A)= 625cm2. Length of base = 123 cm.
We know, Area of triangle = 1/2 * Base * Height
∴ 625 = 1/2 * 125 * H
=1250/125
⇒ H = 10 cm.
Ex 8: The perimeter of an isosceles right-angled triangle is 20 meters. Find its area.
Sol: In case of an isosceles right angled triangle, Base = Height. Let “x” be the base and “y” be the hypotenuse.
∴ x + x + y = 20 ⇒ 2x + y = 20 ….(eqn 1)
Also y2= x2 + x2
⇒ y2=2 x2
∴ y = √ 2 x
2x + √ 2 x = 20 using …..(eqn 1)
⇒ 3.41 x = 20
∴ x = 5.86m.
Area = 1/2 x2 = 1/2 * 5.86 * 5.86
Hence, the required area =17.16 m2
Related Videos:
Frequently Asked Questions
Q1: How to determine the area of a triangle with length of three sides provided?
Ans: When the length of the three sides of the triangle are given, then the area of that triangle can calculated by using Heron's Formula. ‘S’ is semi-perimeter.
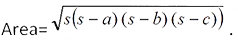
Q2: How to determine area of triangle provided with length of base and height?
Ans: For a given triangle, where base of the triangle is b and height is h, the area of the triangle can be determined by the recipe, such as;
A = ½ (b × h) sq. units
Q3: How to calculate the area of a triangle using vectors?
Ans: Suppose vectors u and v are framing a triangle in space. At that point, the area of this triangle is equivalent to half of the size of the result of these two vectors, such that,
A = ½ |u + v|
Important Chapters:


Area = 96cm2.
Base (B) – Height (H) = 4.
Also, 1/2 Base . Height = 96 cm2
∴ H (H – 4) = 192
⇒ Height = 16 cm and Base length = 12 cm
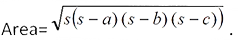
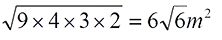
Considering the length of equal side = x.
∴ x + x + 30 = 100 cm
⇒ 2x = 70
We know, Area of triangle = 1/2 * Base * Height
∴ 625 = 1/2 * 125 * H
⇒ H = 10 cm.
∴ x + x + y = 20 ⇒ 2x + y = 20 ….(eqn 1)
Also y2= x2 + x2
⇒ y2=2 x2
∴ y = √ 2 x
∴ x = 5.86m.
Area = 1/2 x2 = 1/2 * 5.86 * 5.86
Hence, the required area =17.16 m2
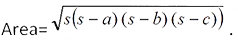
Similar Questions
Knowledge Check
- Question 1 - Select One
If ! denote the area of any triangle with semi-perimeter , then
A!<s22B!>s24C!<s24D!<s2 - Question 2 - Select One
The medians of a triangle ABC meet at G. If the area of the triangle be 120 sq cm, then the area of the triangle GBC is
A30 sq.cmB50 sq. cmC20 sq.cmD40 sq.cm - Question 3 - Select One
The height of an equilateral triangle is 15 cm.The area of the triangle is
A50√3 sq cmB70√3 sq cmC75√3 sq cmD150√3 sq cm
G is the centroid of the triangle ABC. Prove that the area of the triangle ABG is one third of the area of the triangle ABC.
View SolutionThe area of the triangle formed by three points on a parabola is how many times the area of the triangle formed by the tangents at these points?
View SolutionFind the area of Fig.34 in the following ways: Sum of the areas of three triangles Area of a rectangle - sum of the areas of five triangles
View SolutionThe height of an equilateral triangle is 15 cm. The area of the triangle is
View SolutionThe height of an equilateral triangle is 6cm. Then the area of the triangle is
View Solution

