A standard unit of volume
A Standard Unit of Volume
In this chapter, we will study units of volume. Students will be able to get the right idea on the standard unit of volume as well as volume calculation. We will also try to look at some examples that would help you to get the better idea about it.
What is volume?
Volume is a basic physical quantity which expresses the three-dimensional limit of an object. Numerically, the volume is often quantified by using the SI derived unit, the cubic metre. It is to be noted that mostly the unit is used in specifying the volume of an object or a liquid. But at the same time, students should know that mass and volume are two different physical quantities.
What are the volume formulas?
Cube = a 3

Rectangular prism = a b c

Irregular prism = b h

Cylinder = b h = pi r 2 h

Pyramid = (1/3) b h
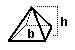
Cone = (1/3) b h = 1/3 pi r 2 h
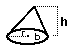
Sphere = (4/3) pi r 3

Ellipsoid = (4/3) pi r1 r2 r3

SI Unit of Volume
When it comes to the SI unit of volume, it is measured in cubic metres. It incorporates the dimensional use of the base unit of metre and length. But it is to be noted that litre is the widely used metric unit for volume. To highlight small or large volume measures, standard metric prefixes are used. Let us look at the table below:
Unit of measure
cubic metre
litre
1 cubic metre
1
1000
1 barrel
= 0.158 987 294 928
= 158.987294928
1 cubic foot
= 0.028 316 846 592
= 28.316864592
1 cubic decimetre
= 0.001
1
1 litre
= 0.001
1
1 gallon (US)
= 0.003 785 411 784
= 3.785411784
1 pint (US)
= 0.000 473 176 473
= 0.473176473
1 cubic inch
= 0.000 016 387 064
= 0.016387064
1 cubic centimetre
= 0.000 001
= 0.0010000
Related Videos:
We will now concentrate on the different solved examples
1. Find the volume of a cuboid whose
(i) length = 10 cm, breadth = 5 cm, height = 3 cm
(ii) length = 1.5 m, breadth = 20 cm, height = 10 cm
(iii) length = 12 cm, breadth = 3.5 dm, height = 7 cm.
Solution:
(i) Here, given
Length of a cuboid = 10 cm
Breadth of a cuboid = 5 cm
Height of a cuboid = 3 cm
By making use of the formula
Volume of a cuboid = length × breadth × height
= 10 × 5 × 3
= 150 cm3
(ii) Here, given
Length of a cuboid = 1.5 m = 150 cm
Breadth of a cuboid = 20 cm
Height of a cuboid = 10 cm
By using the formula
Volume of a cuboid = length × breadth × height
= 150 × 20 × 10
= 54000 cm3
(iii) Here, given
Length of a cuboid = 12 cm
Breadth of a cuboid = 3.5 dm = 35 cm
Height of a cuboid = 7 cm
By using the formula
Volume of a cuboid = length × breadth × height
= 12 × 35 × 7
= 2940 cm3
Question: A cuboidal vessel is 30 cm long and 10 cm wide. Can you calculate as to how high it must be made so that it can hold 600 cm3 of a liquid?
Solution: Here, given,
Volume of a liquid in the vessel = 600 cm3
Length of a cuboidal vessel = 30 cm
Breadth of a cuboidal vessel = 10 cm
Let us assume height of cuboidal vessel be ‘h’ cm
We know that, l × b × h = 600 cm3
h = 600/(l × b)
= 600/(30 × 10 )
= 2 cm
So, the height should be 2 cm.
Question: The length of a milk container is 10 cm long and 40 cm wide. Can you calculate as to what should be its height so that it can hold 8 litres of milk?
Solution: Here, given,
Volume = 8 litres = 8000 cm3
Length of a milk container = 10 cm
Breadth of a milk container = 40 cm
Let us assume the height of milk container be ‘h’ cm
We know that, l × b × h = 8000 cm3
h = 8000/ (l × b)
= 8000/ (10× 40 )
= 20cm
So, the height should be 20 cm.
Question: An ice-cream brick measures 30 cm by 20 cm by 7 cm. How many such bricks can be stored in deep fridge whose inner dimensions are 100 cm by 45 cm by 43 cm?
Solution:
Here, given,
Dimensions of ice cream brick = 30 cm × 20cm × 7cm
Dimensions of fridge is = 100 cm × 45cm × 43 cm
So,
Number of bricks that can be put in fridge = volume of fridge / volume of one ice brick
= (100 × 45 × 43) / (30 × 20 × 7)
= 47 ice cream bricks
Question: Find the volume in cubic decimetre of each of the cubes whose side is
(i) 1.5 m
(ii) 75cm
(iii) 2 dm 5 cm
Solution:
(i) Given details are,
Side of cube = 1.5m = 15 dm
So, Volume of cube = 153 = 3375 dm3
(ii) Given details are,
Side of cube = 75cm = 7.5 dm
So, volume of cube = 7.53 = 421.875 dm3
(iii) Given details are,
Side of cube = 2dm 5cm = 2.5 dm
So, volume of cube = 2.53 = 15.625 dm3
Question: A classroom is 11 m long, 8 m wide and 5 m high. Find the sum of the areas of its floor and the four walls (including doors, windows etc.)
Solution:
Here, given,
Dimensions of class room = 11m × 8m × 5m
Where, Length = 11m, Breadth = 8m, Height = 5m
We know,
Area of floor = length × breadth
= 11 × 8
= 88 m2
Area of four walls (including doors & windows) = 2 (lh + bh) cm2
= 2 (11×5 + 8×5)
= 2 (55 + 40)
= 2 (95)
= 190m2
∴ Sum of areas of floor and four walls = area of floor + area of four walls
= 88 + 190
= 278 m2
Important Chapters:




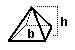
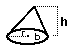


Unit of measure
cubic metre
litre
1 cubic metre
1
1000
1 barrel
= 0.158 987 294 928
= 158.987294928
1 cubic foot
= 0.028 316 846 592
= 28.316864592
1 cubic decimetre
= 0.001
1
1 litre
= 0.001
1
1 gallon (US)
= 0.003 785 411 784
= 3.785411784
1 pint (US)
= 0.000 473 176 473
= 0.473176473
1 cubic inch
= 0.000 016 387 064
= 0.016387064
1 cubic centimetre
= 0.000 001
= 0.0010000
(i) length = 10 cm, breadth = 5 cm, height = 3 cm
(ii) length = 1.5 m, breadth = 20 cm, height = 10 cm
(iii) length = 12 cm, breadth = 3.5 dm, height = 7 cm.
(iii) 2 dm 5 cm
Similar Questions
Knowledge Check
The standard unit of value, used as medium of exchange during the Vedic period, was :
ACowBNecklet of gold (niska)CBoth (a) and (b)DPanaThe standard unit of measuring an angle is ......... .
AcmBkmCmmDdegreeThe standard unit of measuring pressure is
AN/m2BPaCkgfDN/kgf
Why can a pace or a footstep not be used as a standard unit of length?
View SolutionIt is desirable that the standards of units be easily available, invariable, indestructible and easily reproducible. If we use foot of a person as a standard unit of length, which of theabove features are present and which are not?
View SolutionThe standard unit of pressure among the following is _______
View SolutionWhat is the standard unit of measurement of pressure?
View SolutionSpecific volume of a particular substance defined as the volume occupied by per unit mass of a particular substance. The standard unit of specific volume is m3/kg
Specific volume =Volume of substanceMass of substance

The above plot shows the variation of specific volume (ml/g) of H2O with the temperature in degree centrigrade.
There are three temperature zone in a lake 2∘C,4∘C and 20∘C the following correctly represent the temperature zone :
View Solution
