Draw a line segment CD . Produce it to CE such that CE=3CD
To solve the problem of drawing a line segment CD and producing it to CE such that CE=3CD, follow these steps:
1. Draw Line Segment CD:
- Use a ruler to draw a line segment CD of any length. For this example, let’s say we draw CD=2 cm.
2. Calculate Length of CE:
- Since CE=3×CD, we need to calculate the length of CE.
- If CD=2 cm, then:
CE=3×2 cm=6 cm
3. Extend Line Segment to Point E:
- From point C, use the ruler to measure and mark a point E such that the length CE is equal to 6 cm.
- To do this, measure 4 cm from point D (since CD=2 cm, and CE=6 cm, the extension from D to E will be CE−CD=6 cm−2 cm=4 cm).
4. Label the Points:
- Ensure that the points are clearly labeled as C, D, and E.
Final Drawing:
- You should have a line segment CD measuring 2 cm, and the extended line segment CE measuring 6 cm, with point E located 4 cm away from point D.
- Use a ruler to draw a line segment CD of any length. For this example, let’s say we draw CD=2 cm.
- Since CE=3×CD, we need to calculate the length of CE.
- If CD=2 cm, then:
CE=3×2 cm=6 cm
- From point C, use the ruler to measure and mark a point E such that the length CE is equal to 6 cm.
- To do this, measure 4 cm from point D (since CD=2 cm, and CE=6 cm, the extension from D to E will be CE−CD=6 cm−2 cm=4 cm).
- Ensure that the points are clearly labeled as C, D, and E.
- You should have a line segment CD measuring 2 cm, and the extended line segment CE measuring 6 cm, with point E located 4 cm away from point D.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram in which BC is produced to E such that CE=BC.AE intersects CD at F. Prove that ar ( ADF)= ar ( ECF) If the area of DFB=3 cm2, find the area of ^(gm) ABCD
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC

View SolutionABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionIn a ABC , point D is on side AB and point E is on side AC , such that BCED is a trapezium. If DE:BC=3:5 , then Area(ADE):Area(BCED)= 3:4 (b) 9:16 (c) 3:5 (d) 9:25
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
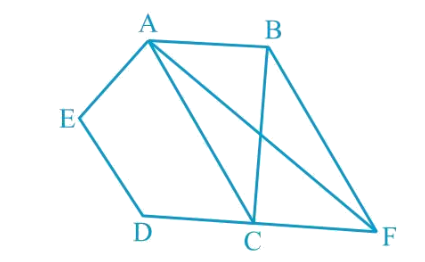
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar(ACB)=ar(ACF) (ii) ar(AEDF)=ar(ABCDE)
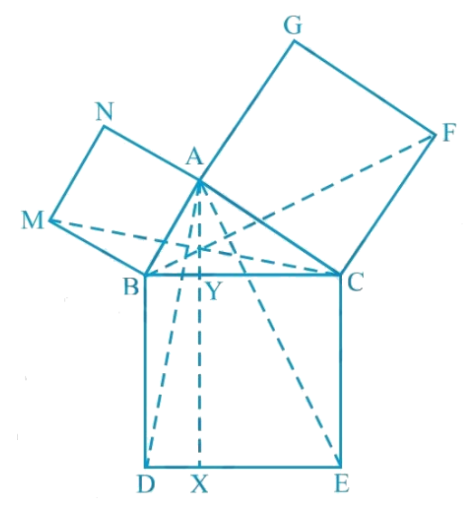
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
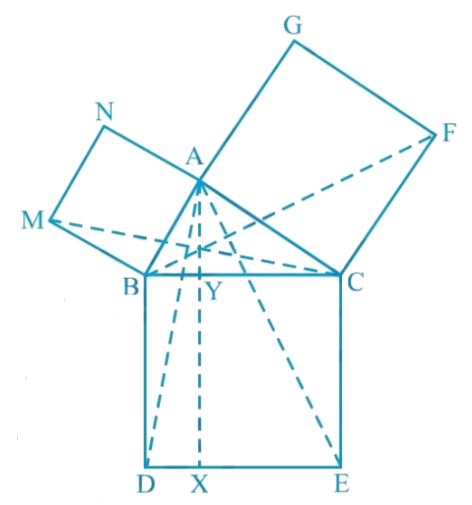
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
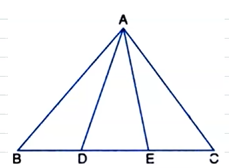
View Solution
