Which of the following statements must be true ? I. The range of a data set must be smaller than its standard deviation.
II. The standard deviation of a data set must be smaller than its mean.
III. The median of a data set must be smaller than its mode.
I only
I and II
II only
none are true
To determine which of the statements must be true, we will analyze each statement one by one, providing examples to prove or disprove them.
Statement I: The range of a data set must be smaller than its standard deviation.
1. Example Dataset: Let's consider the dataset: 1, 5, 10.
2. Calculate the Mean:
Mean=1+5+103=163≈5.33
3. Calculate the Range:
Range=Maximum−Minimum=10−1=9
4. Calculate the Standard Deviation:
- First, find the squared differences from the mean:
- (1−5.33)2=18.75
- (5−5.33)2=0.11
- (10−5.33)2=21.81
- Sum of squared differences:
18.75+0.11+21.81=40.67
- Divide by the number of elements:
40.673≈13.56
- Take the square root:
Standard Deviation≈√13.56≈3.68
5. Comparison:
- Range (9) is greater than Standard Deviation (3.68).
- Therefore, Statement I is false.
Statement II: The standard deviation of a data set must be smaller than its mean.
1. Example Dataset: Let's consider the dataset: 0, 0, 7, 10.
2. Calculate the Mean:
Mean=0+0+7+104=174=4.25
3. Calculate the Standard Deviation:
- First, find the squared differences from the mean:
- (0−4.25)2=18.0625
- (0−4.25)2=18.0625
- (7−4.25)2=7.5625
- (10−4.25)2=33.0625
- Sum of squared differences:
18.0625+18.0625+7.5625+33.0625=76.75
- Divide by the number of elements:
76.754=19.1875
- Take the square root:
Standard Deviation≈√19.1875≈4.38
4. Comparison:
- Standard Deviation (4.38) is greater than Mean (4.25).
- Therefore, Statement II is false.
Statement III: The median of a data set must be smaller than its mode.
1. Example Dataset: Let's consider the dataset: 1, 2, 3, 4.
2. Calculate the Median:
- Since there are four elements, the median is the average of the two middle numbers (2 and 3):
Median=2+32=2.5
3. Calculate the Mode:
- In this dataset, all numbers occur only once, so there is no mode. However, if we modify the dataset to 1, 1, 2, 3, 4, the mode would be 1.
- Here, Median (2.5) is greater than Mode (1).
- Therefore, Statement III is false.
Conclusion:
All three statements are false. Therefore, the answer to the question is that none of the statements must be true.
---
2. Calculate the Mean:
Mean=1+5+103=163≈5.33
3. Calculate the Range:
Range=Maximum−Minimum=10−1=9
4. Calculate the Standard Deviation:
- First, find the squared differences from the mean:
- (1−5.33)2=18.75
- (5−5.33)2=0.11
- (10−5.33)2=21.81
- Sum of squared differences:
18.75+0.11+21.81=40.67
- Divide by the number of elements:
40.673≈13.56
- Take the square root:
Standard Deviation≈√13.56≈3.68
5. Comparison:
- Range (9) is greater than Standard Deviation (3.68).
- Therefore, Statement I is false.
2. Calculate the Mean:
Mean=0+0+7+104=174=4.25
3. Calculate the Standard Deviation:
- First, find the squared differences from the mean:
- (0−4.25)2=18.0625
- (0−4.25)2=18.0625
- (7−4.25)2=7.5625
- (10−4.25)2=33.0625
- Sum of squared differences:
18.0625+18.0625+7.5625+33.0625=76.75
- Divide by the number of elements:
76.754=19.1875
- Take the square root:
Standard Deviation≈√19.1875≈4.38
4. Comparison:
- Standard Deviation (4.38) is greater than Mean (4.25).
- Therefore, Statement II is false.
2. Calculate the Median:
- Since there are four elements, the median is the average of the two middle numbers (2 and 3):
Median=2+32=2.5
3. Calculate the Mode:
- In this dataset, all numbers occur only once, so there is no mode. However, if we modify the dataset to 1, 1, 2, 3, 4, the mode would be 1.
- Here, Median (2.5) is greater than Mode (1).
- Therefore, Statement III is false.
All three statements are false. Therefore, the answer to the question is that none of the statements must be true.
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - STATISTICSEXERCISE - EXERCISES8videos
STATISTICS
- BOOK - ENGLISH SATCHAPTER - SOLVING POLYNOMIAL INEQUALITIES EXERCISE - EXERCISES3videos
SOLVING POLYNOMIAL INEQUALITIES
- BOOK - ENGLISH SATCHAPTER - STRATEGIES FOR SOLVING SAT MATH PROBLEMS EXERCISE - EXAMPLE19videos
STRATEGIES FOR SOLVING SAT MATH PROBLEMS
Similar Questions
Knowledge Check
- Question 1 - Select One
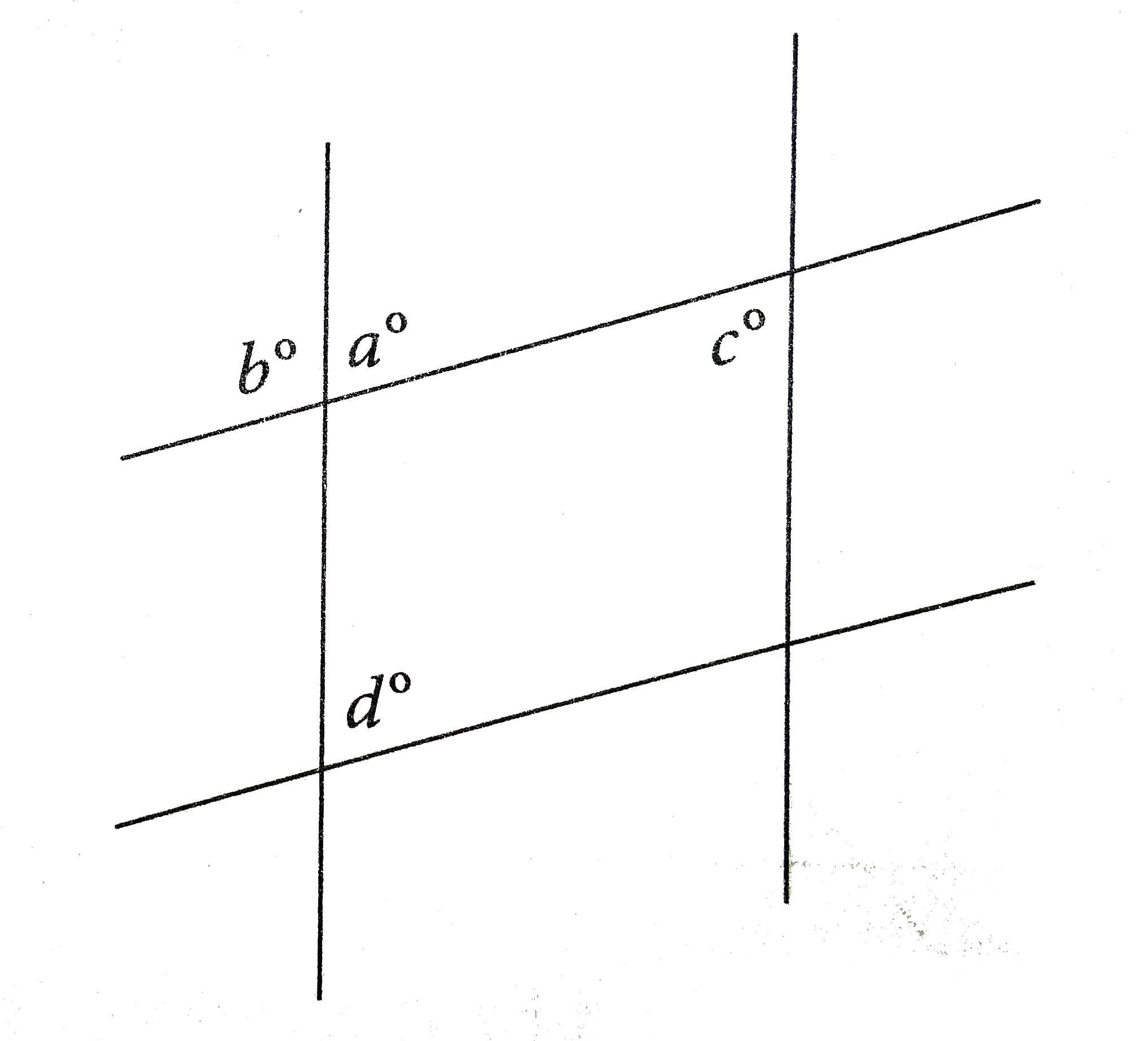
Which of the following statements must be true?
I. a+b<180
II. a+d=180
III.a+d>180ANoneBII onlyCI and II onlyDII and III only - Question 2 - Select One
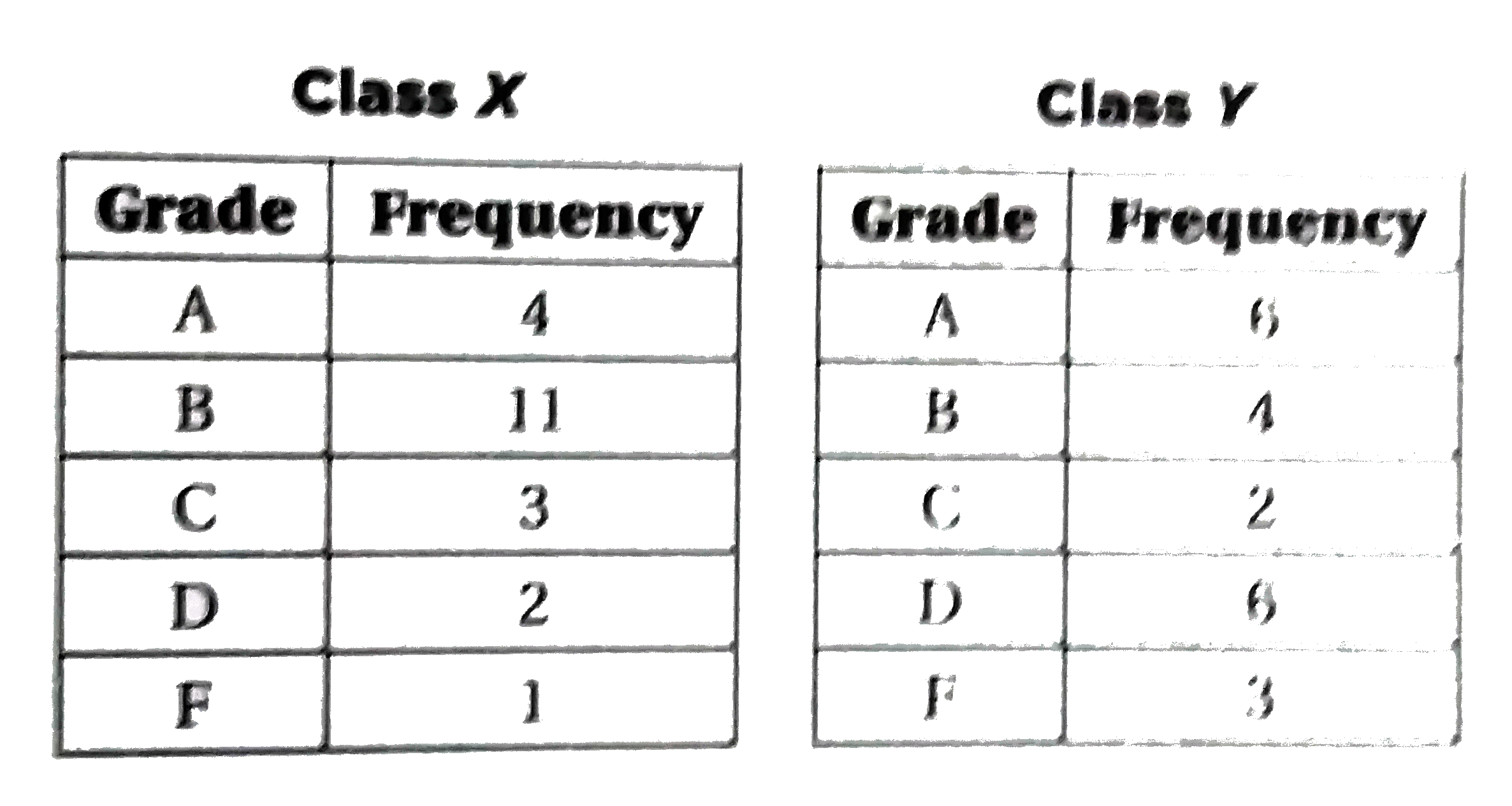
The tables give the distribution of grades for 21 students in two different college mathematics classes. For purposes of making statistical calculations, A=4,B=3,C=2,D=1,andF=0. Which of the following statements is true about the data shown for these two classes?
I. The standard deviation of grades is greater for class X.
II. the standard deviation of grades is greater for class Y.
III. The median letter grade is the same for classes X and Y.AI onlyBII onlyCI and III onlyDII and III only - Question 3 - Select One
Which of the following must be true?
(I) The area of triangle P.
(II) The area of triangle Q.
(III) The area of triangle R.
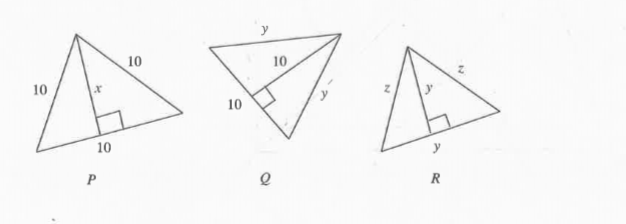 AI = II = IIIBI lt II lt IIICI gt II lt IIIDIII lt I lt II
AI = II = IIIBI lt II lt IIICI gt II lt IIIDIII lt I lt II
An data set has a mean of 12 and a standard deviation of 2. If 5 is added to twice each data value, the new data set has
View SolutionThe mean of a finite set S of numbers is 14, the median of this set of numbers is 12, and the standard deviation is 1.8. A new set T is formed by multiplying each member of the set S by 3. Which of the following statements must be true of the set T ?
I. The mean of the numbers in set T is 42.
II. The median of the numbers in set T is 36.
III. The standard deviation of the numbers in set T is 5.4.View SolutionWhich of the following must always be true ?
I. If an object's acceleration is constant, then it must move in a striaght line.
II. If an object's acceleration is zero, then its speed must remain constant.
III. If an object's speed remains constant, then its acceleration must be zero.View Solution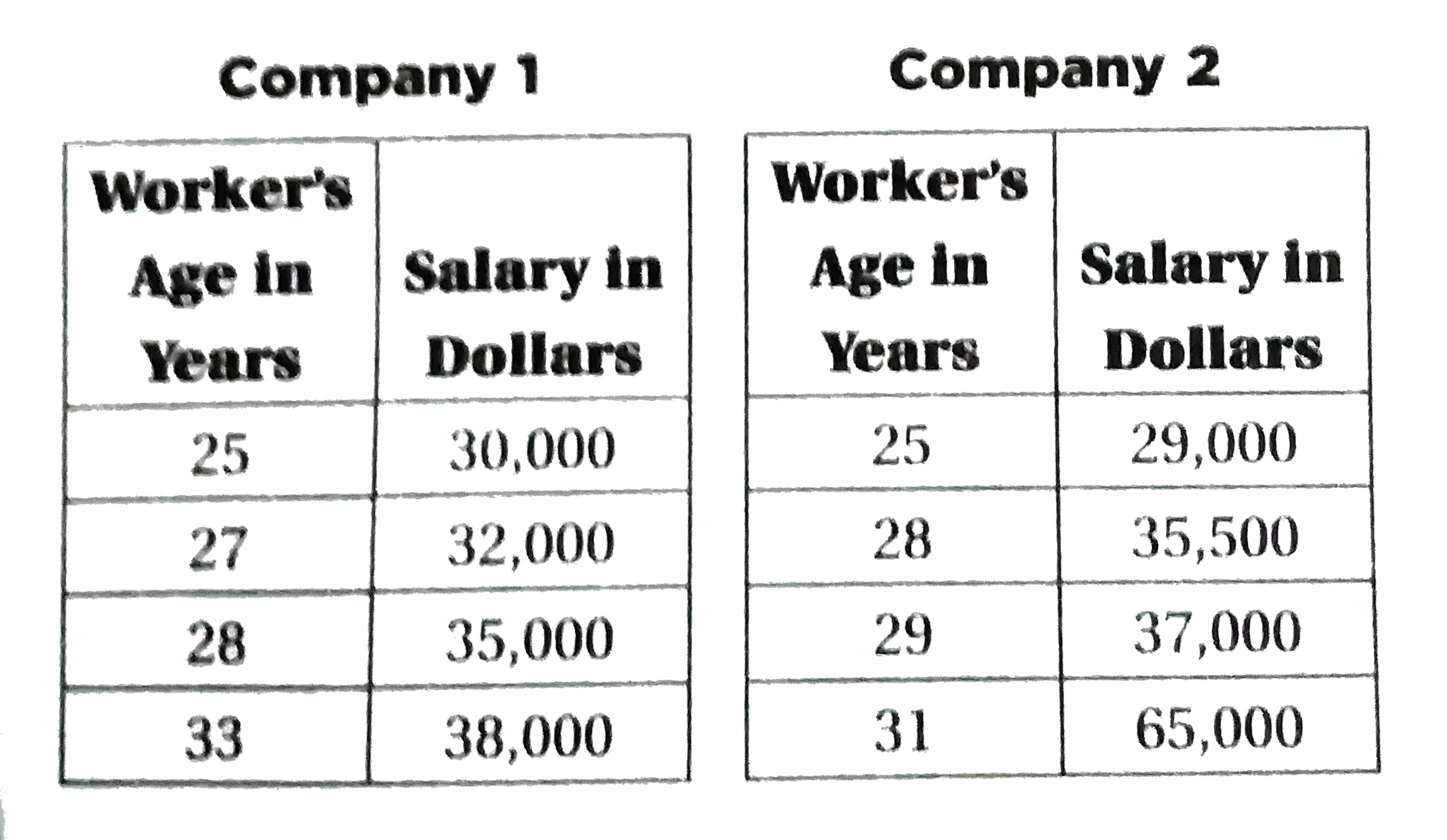
Which of the following statements is true about the data in the tables above?
I. The mean salaries for both companies are greater than $35,000.
II. The mean age of workers in Comapy 1 is greater than the mean age of workers in Company 2.
III. The salary range in Company 2 is greater than the salary range in Company 1.View Solution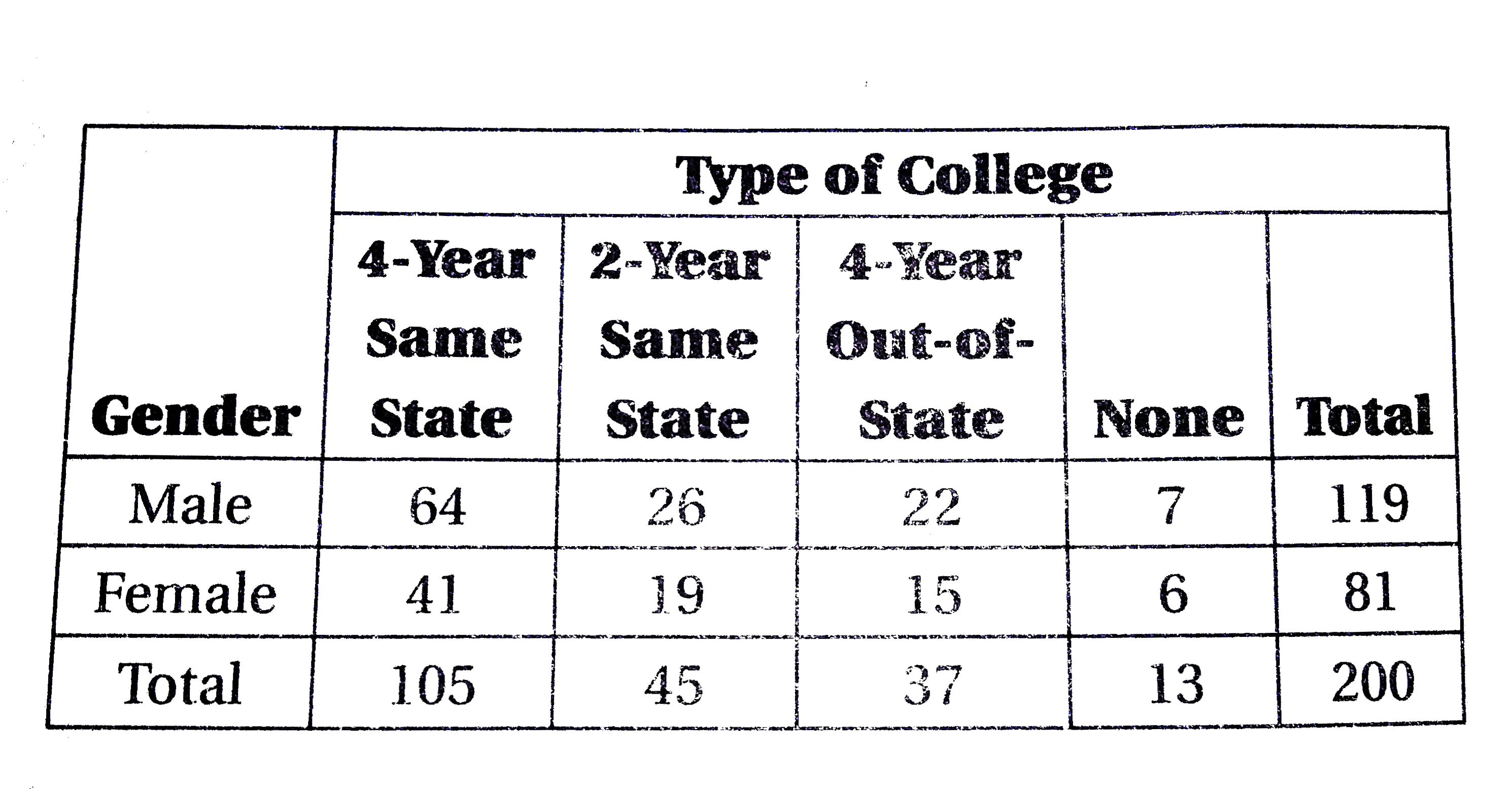
Based on the data in the table above, which of the following statements must be true?
I. For every 3 men who applied to a same state collage, 2 women applied to a same state collage.
II. If a female student is selected at random the probability that she did not apply to a 2-year collage is greater than 75%.
III. Of the students who applied to a same state collage, 40 % were femalesView Solution

