If the range of a set of integers is 2 and the mean is 50, which of the following statements must be true?
I. The mode is 50.
II. The median is 50.
III. There are exactly three data value.
only I
only II
only III
I and II
The correct Answer is:B
To solve the problem, we need to analyze the given statements based on the conditions provided: the range of a set of integers is 2, and the mean is 50.
1. Understanding the Range:
- The range is defined as the difference between the largest and smallest values in the dataset.
- Given that the range is 2, if we let the smallest value be x, then the largest value must be x+2.
2. Identifying Possible Values:
- The integers in the dataset must include x (smallest), x+1, and x+2 (largest).
- Therefore, the possible values in the dataset could be x,x+1,x+2.
3. Calculating the Mean:
- The mean is given as 50. The mean of a set of numbers is calculated as the sum of the numbers divided by the count of the numbers.
- For the integers x, x+1, and x+2, the mean can be calculated as:
Mean=x+(x+1)+(x+2)3=3x+33=x+1
- Setting this equal to the given mean:
x+1=50⟹x=49
- Therefore, the values in the dataset must be 49,50,51.
4. Evaluating the Statements:
- Statement I: The mode is 50.
- The mode is the most frequently occurring number in the dataset. In our case, we have 49,50,51 each occurring once, so there is no mode. This statement is not necessarily true.
- Statement II: The median is 50.
- The median is the middle value when the numbers are arranged in order. For the dataset 49,50,51, the median is indeed 50. This statement is true.
- Statement III: There are exactly three data values.
- While we have identified three values 49,50,51, the conditions do not restrict the dataset to exactly three values. We could have more occurrences of 49 or 51, so this statement is not necessarily true.
5. Conclusion:
- Based on the evaluations:
- Statement I is false.
- Statement II is true.
- Statement III is false.
- Therefore, the only statement that must be true is Statement II.
Final Answer:
The correct answer is only statement II is true.
- The range is defined as the difference between the largest and smallest values in the dataset.
- Given that the range is 2, if we let the smallest value be x, then the largest value must be x+2.
- The integers in the dataset must include x (smallest), x+1, and x+2 (largest).
- Therefore, the possible values in the dataset could be x,x+1,x+2.
- The mean is given as 50. The mean of a set of numbers is calculated as the sum of the numbers divided by the count of the numbers.
- For the integers x, x+1, and x+2, the mean can be calculated as:
Mean=x+(x+1)+(x+2)3=3x+33=x+1
- Setting this equal to the given mean:
x+1=50⟹x=49
- Therefore, the values in the dataset must be 49,50,51.
- Statement I: The mode is 50.
- The mode is the most frequently occurring number in the dataset. In our case, we have 49,50,51 each occurring once, so there is no mode. This statement is not necessarily true.
- Statement II: The median is 50.
- The median is the middle value when the numbers are arranged in order. For the dataset 49,50,51, the median is indeed 50. This statement is true.
- Statement III: There are exactly three data values.
- While we have identified three values 49,50,51, the conditions do not restrict the dataset to exactly three values. We could have more occurrences of 49 or 51, so this statement is not necessarily true.
- Based on the evaluations:
- Statement I is false.
- Statement II is true.
- Statement III is false.
- Therefore, the only statement that must be true is Statement II.
The correct answer is only statement II is true.
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - STATISTICSEXERCISE - EXERCISES8videos
STATISTICS
- BOOK - ENGLISH SATCHAPTER - SOLVING POLYNOMIAL INEQUALITIES EXERCISE - EXERCISES3videos
SOLVING POLYNOMIAL INEQUALITIES
- BOOK - ENGLISH SATCHAPTER - STRATEGIES FOR SOLVING SAT MATH PROBLEMS EXERCISE - EXAMPLE19videos
STRATEGIES FOR SOLVING SAT MATH PROBLEMS
Similar Questions
Knowledge Check
- Question 1 - Select One
If x is integer and x2 is even, which of the following must be true?
Ax is evenBx is oddCx3 is oddDx3 is even - Question 2 - Select One
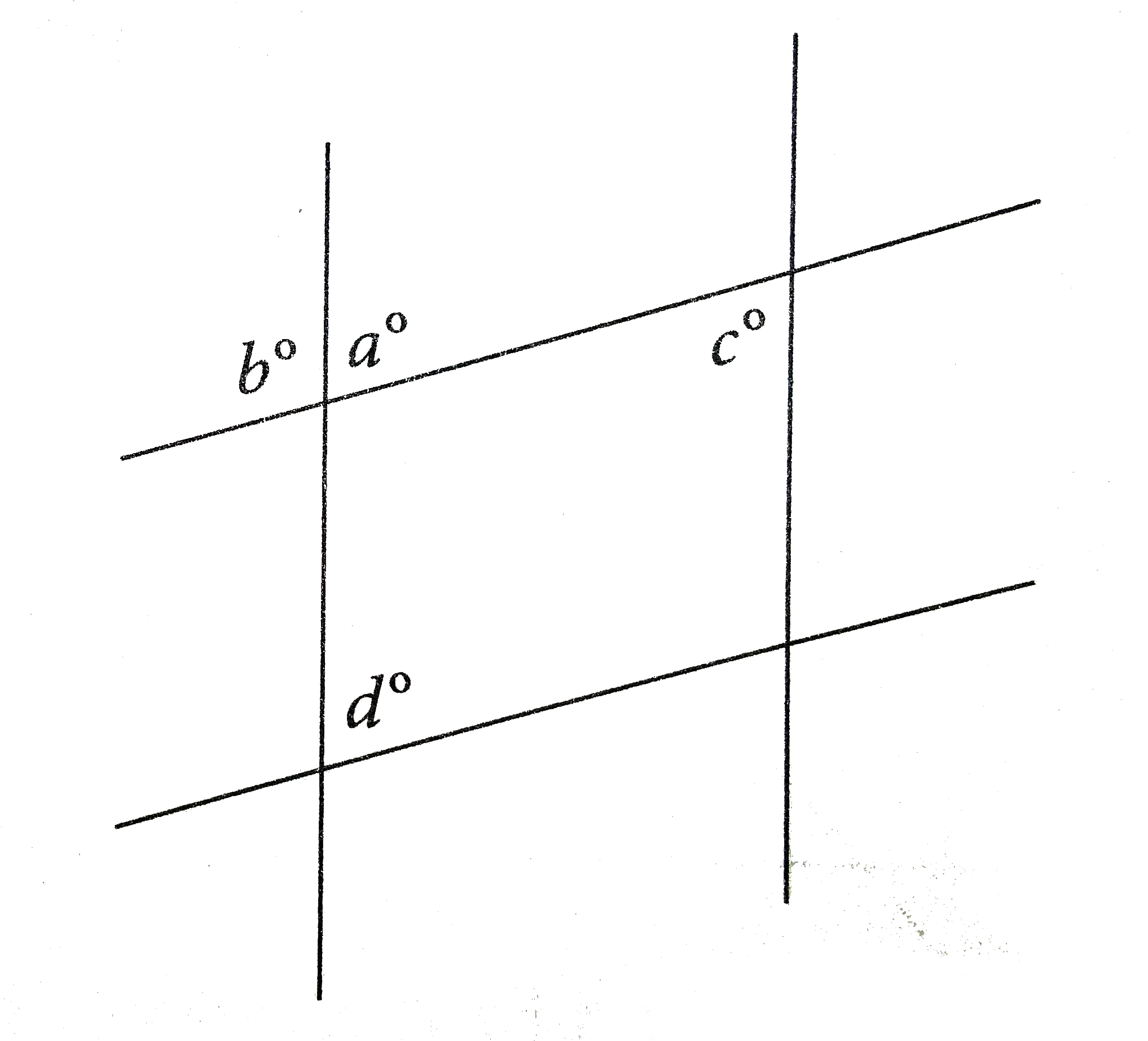
Which of the following statements must be true?
I. a+b<180
II. a+d=180
III.a+d>180ANoneBII onlyCI and II onlyDII and III only - Question 3 - Select One
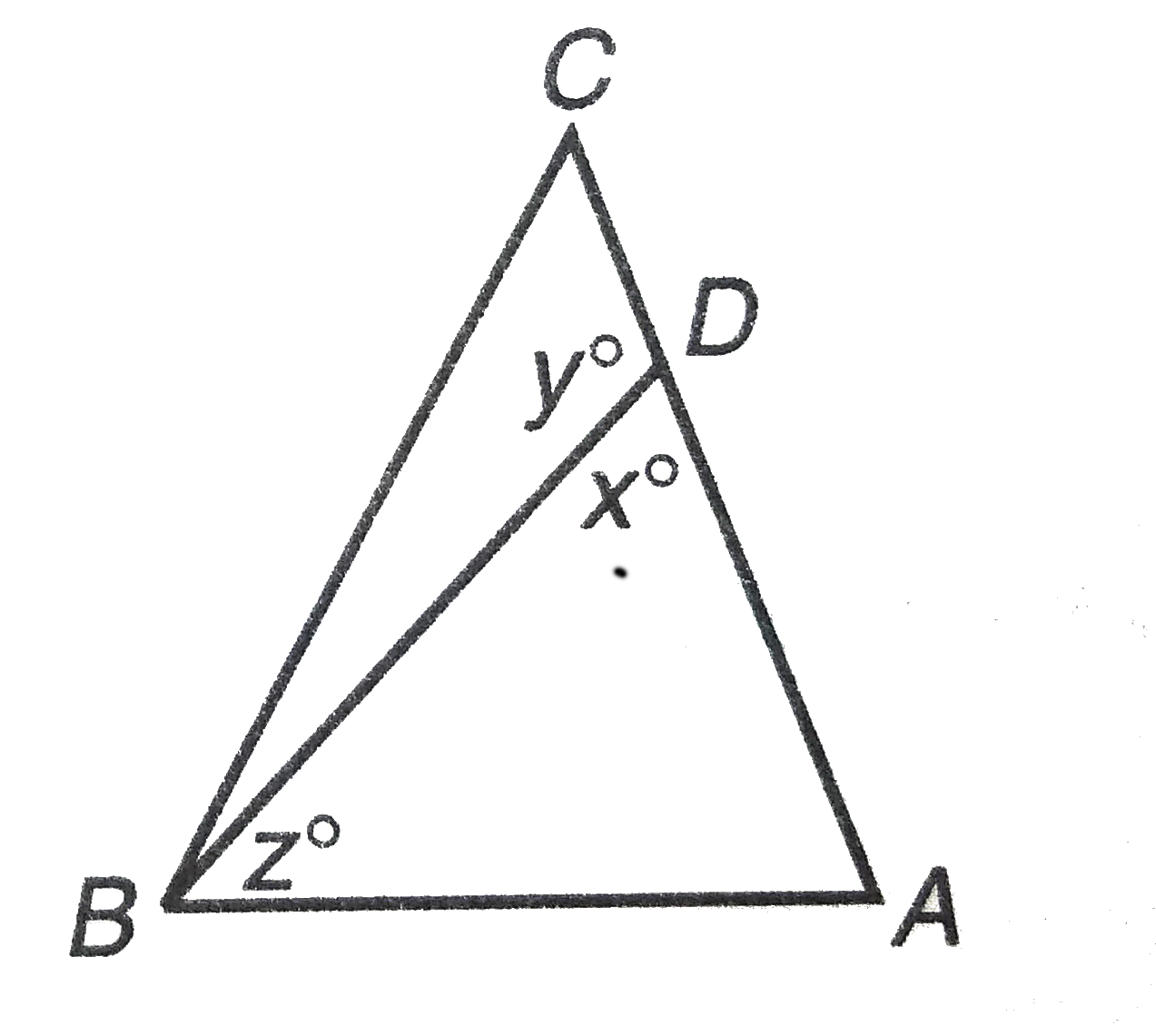
In △ABC, if AB=CD, which of the following statements must be true?
I.x>z
II. y>x
III. AB>BCAI onlyBII onlyCI and II onlyDII and III only
Which of the following statements is not true of two genes that show 50% recombination frequency?
View SolutionIf a=3+b, which of the following must be true?
I. a>b+2.5
II. a<b+2.5
III. a>2+bView SolutionWhich of the following must be true?
(I) The area of triangle P.
(II) The area of triangle Q.
(III) The area of triangle R.
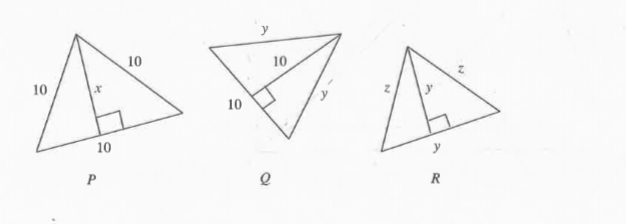 View Solution
View SolutionGiven the set of data 1,1,2,2,2,3,3,4, which one of the following statements is true?
View SolutionWhich of the following is equal to i50+i0?
View Solution

