Draw two parallel lines at a distance 5 cm apart.
To draw two parallel lines at a distance of 5 cm apart, follow these steps:
Step 1: Draw the First Line
- Use a ruler to draw a straight horizontal line. Label this line as PQ.
Hint: Make sure the line is straight and long enough to allow for the second line to be drawn parallel to it.
Step 2: Mark Two Points on the First Line
- Choose two points on line PQ. Label them as point A and point B.
Hint: You can choose any two points on the line, but make sure they are not too close to each other for better accuracy.
Step 3: Draw Arcs from Points A and B
- With a compass, place the pointer on point A and draw an arc above and below the line PQ.
- Without changing the compass width, place the pointer on point B and draw another arc above and below the line PQ.
Hint: Ensure that the compass width is the same for both arcs to maintain symmetry.
Step 4: Draw Perpendicular Lines
- From the points where the arcs intersect above and below line PQ, draw two perpendicular lines (90 degrees) from points A and B. Extend these lines upwards.
Hint: You can use a protractor to measure the 90-degree angle accurately.
Step 5: Measure 5 cm from Points A and B
- With the compass set to a width of 5 cm, place the pointer on point A and draw an arc on the perpendicular line above point A.
- Repeat this step for point B.
Hint: Make sure the compass is set exactly to 5 cm for accuracy.
Step 6: Mark the Intersection Points
- Label the points where the arcs intersect the perpendicular lines as points C and D.
Hint: These points C and D will help you create the second parallel line.
Step 7: Draw the Second Parallel Line
- Use a ruler to draw a straight line connecting points C and D. This line will be parallel to line PQ and will be 5 cm apart from it.
Hint: Double-check that the distance between line PQ and line CD is exactly 5 cm.
Final Result
You now have two parallel lines PQ and CD that are 5 cm apart.
---
- Use a ruler to draw a straight horizontal line. Label this line as PQ.
- Choose two points on line PQ. Label them as point A and point B.
- With a compass, place the pointer on point A and draw an arc above and below the line PQ.
- Without changing the compass width, place the pointer on point B and draw another arc above and below the line PQ.
- From the points where the arcs intersect above and below line PQ, draw two perpendicular lines (90 degrees) from points A and B. Extend these lines upwards.
- With the compass set to a width of 5 cm, place the pointer on point A and draw an arc on the perpendicular line above point A.
- Repeat this step for point B.
- Label the points where the arcs intersect the perpendicular lines as points C and D.
- Use a ruler to draw a straight line connecting points C and D. This line will be parallel to line PQ and will be 5 cm apart from it.
You now have two parallel lines PQ and CD that are 5 cm apart.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a trapezium, the two non-parallel sides are equal in length, each being of 5 units. The parallel sides are at a distance of 3 units apart. If the smaller side of the parallel sides is of length 2 units, then the sum of the diagonals of the trapezium is
A10√5 unitsB6√5 unitsC5√5 unitsD3√5 unitsA radius of circle is 2.5cm AB and CD two parallel chords are at distance of 2.7cm. It AB=4.8cm, then value of CD is
A4.8cmB2.4cmC3cmD4cmThe figure shows two parallel plane mirrors placed 10cm apart. An object O is placed 7cm from mirror M1. Then the distance of final image formed from mirror M1 is:
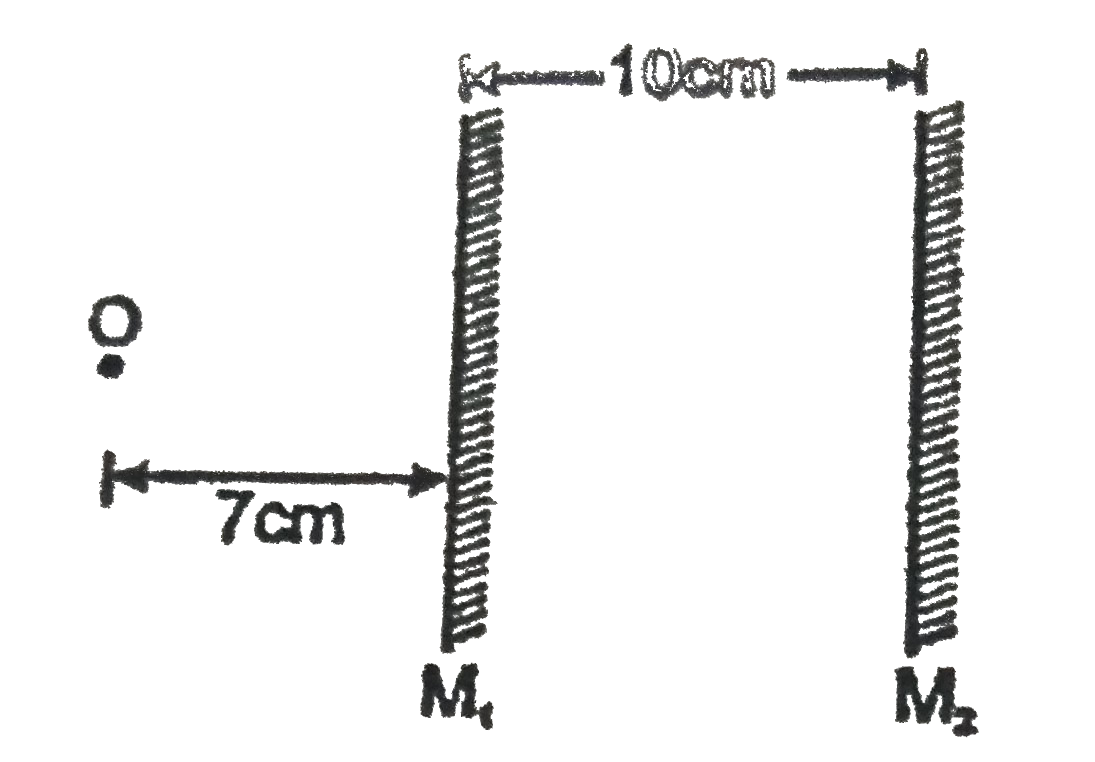 A7cmB13 cmC14 cmD∞
A7cmB13 cmC14 cmD∞
Pand Q are two like parallel forces. If two equal and opposite forces S, in any two parallel lines at a distance: b apart in the plane of Pand Q, are combined with them, then their resultant is displaced by a distance bSP+Q.
View SolutionDraw a line PQ . Draw another line parallel to PQ at a distance of 3 cm from it.
View SolutionWhich of the following statements are true and which are false ?
Two parallel lines are everwhere the same distance apart.
View SolutionWrite the equation of a line parallel to X-axis and at a distance 3 cm above it.
View SolutionTwo charges +20μC and −20μC are 5 mm apart. Find the electric field on axial as well as on the equatorial line at a distance 20 cm from the mid -point of the dipole.
View Solution
