Draw ABC in which AB=4.5 cm, BC=5 cm and CA=6 cm. Also, draw the perpendicular bisector of BC.
To construct triangle ABC with the given side lengths AB = 4.5 cm, BC = 5 cm, and CA = 6 cm, and to draw the perpendicular bisector of BC, follow these steps:
1. Draw Line Segment AB:
- Use a ruler to draw a line segment AB that measures 4.5 cm.
- Label the endpoints as A and B.
Hint: Make sure to measure accurately using the ruler to get the correct length.
2. Construct Circle with Center A:
- Using a compass, set the width to 6 cm (the length of CA).
- Place the compass point on A and draw an arc above and below the line segment AB.
Hint: The arc should extend above and below the line segment to help locate point C.
3. Construct Circle with Center B:
- Adjust the compass width to 5 cm (the length of BC).
- Place the compass point on B and draw another arc that intersects the previous arcs drawn from A.
Hint: Ensure that the compass is set to the correct width before drawing the arc.
4. Locate Point C:
- The intersection points of the two arcs are the possible locations for point C. Choose one of the intersection points and label it as C.
Hint: You can choose either intersection point, but ensure that it is above or below line AB consistently.
5. Draw Line Segments AC and BC:
- Use a ruler to draw line segments AC and BC.
- Label the segments accordingly.
Hint: Check that the lengths of AC and BC match the given measurements.
6. Draw the Perpendicular Bisector of BC:
- Find the midpoint of line segment BC by measuring its length and dividing it by 2.
- Mark the midpoint and label it as M.
- Using a compass, set the width to more than half the length of BC and draw arcs above and below the line segment BC from points B and C.
- Draw a straight line through the intersection points of the arcs. This line is the perpendicular bisector of BC.
Hint: The perpendicular bisector should intersect BC at a right angle, so ensure your arcs are drawn correctly.
Final Diagram:
You should now have triangle ABC with the sides AB, BC, and CA drawn accurately, along with the perpendicular bisector of BC.
- Use a ruler to draw a line segment AB that measures 4.5 cm.
- Label the endpoints as A and B.
- Using a compass, set the width to 6 cm (the length of CA).
- Place the compass point on A and draw an arc above and below the line segment AB.
- Adjust the compass width to 5 cm (the length of BC).
- Place the compass point on B and draw another arc that intersects the previous arcs drawn from A.
- The intersection points of the two arcs are the possible locations for point C. Choose one of the intersection points and label it as C.
- Use a ruler to draw line segments AC and BC.
- Label the segments accordingly.
- Find the midpoint of line segment BC by measuring its length and dividing it by 2.
- Mark the midpoint and label it as M.
- Using a compass, set the width to more than half the length of BC and draw arcs above and below the line segment BC from points B and C.
- Draw a straight line through the intersection points of the arcs. This line is the perpendicular bisector of BC.
You should now have triangle ABC with the sides AB, BC, and CA drawn accurately, along with the perpendicular bisector of BC.
Topper's Solved these Questions
Similar Questions
Draw a triangle ABC with AB=6 cm, BC=7 cm and CA=8 cm. Using ruler and compass alone, draw (i) the bisector AD of ∠A and (ii) perpendicular AL from A on BC. Measure LAD.
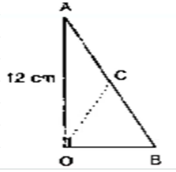
View SolutionIn Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
View SolutionABC is a triangle with B as right angle, AC=5 cm and AB=4 cm. A circle is drawn with A as centre and AC as radius. The length of the chord of this circle passing through C and B is 3 cm (b) 4 cm (c) 5 cm (d) 6 cm
In right , △ABC,∠B=900
AC=5cm,AB=4cm
BC2=AC2−AB2
52−42=25−16=9
BC2=9,BC=3cm
Length of chord,BC=3cm
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionTriangle ABC is right angled at A.AD is perpendicular to BC. If AB=5 cm, BC=13 cm and AC=12 cm. Find the area of ABC. Also, find the length of AD.
View SolutionA paper is in the form of a rectangle ABCD in which AB=20 cm and BC=14 cm. A semicircular portion with BC as diameter is cut off. Find the area of the remaining part.
View SolutionIn Fig.42, ABCD is a parallelogram in which AD=21 cm, DH=18 cm and DK=27 cm. The perimeter of the parallelogram is 105 cm (b) 84.5 cm 169 cm (d) 52.5 cm
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View Solution
