The lines y=ax+bany=bx+a are graphed in the xy-plane. If a and b are non-zero constants and a+b=0, which statements must be true?
The lines are parallel
The lines intersect at right angled
The lines have the same x-intercept.
The lines have the same y-intercept.
The correct Answer is:C
To solve the problem, we need to analyze the given equations of the lines and the condition that a+b=0.
Step 1: Write down the equations of the lines
The equations given are:
1. y=ax+b
2. y=bx+a
Step 2: Substitute the condition a+b=0
From the condition a+b=0, we can express b in terms of a:
b=−a
Step 3: Substitute b into the second equation
Now, substitute b=−a into the second equation:
y=(−a)x+a
This simplifies to:
y=−ax+a
Step 4: Rewrite both equations
Now we have:
1. y=ax+b (where b is still b)
2. y=−ax+a
Step 5: Find the x-intercepts of both lines
To find the x-intercepts, we set y=0 in both equations.
For the first equation:
0=ax+b⟹ax=−b⟹x=−ba
For the second equation:
0=−ax+a⟹−ax=−a⟹x=1
Step 6: Analyze the x-intercepts
Since we have a+b=0 or b=−a, we can substitute b into the x-intercept of the first equation:
x=−−aa=1
Thus, both lines have the same x-intercept, which is x=1.
Step 7: Conclusion
The lines y=ax+b and y=bx+a intersect at the same x-intercept, which is x=1.
Final Answer
The statement that must be true is: The lines have the same x-intercept.
---
The equations given are:
1. y=ax+b
2. y=bx+a
From the condition a+b=0, we can express b in terms of a:
b=−a
Now, substitute b=−a into the second equation:
y=(−a)x+a
This simplifies to:
y=−ax+a
Now we have:
1. y=ax+b (where b is still b)
2. y=−ax+a
To find the x-intercepts, we set y=0 in both equations.
0=ax+b⟹ax=−b⟹x=−ba
0=−ax+a⟹−ax=−a⟹x=1
Since we have a+b=0 or b=−a, we can substitute b into the x-intercept of the first equation:
x=−−aa=1
The lines y=ax+b and y=bx+a intersect at the same x-intercept, which is x=1.
The statement that must be true is: The lines have the same x-intercept.
Topper's Solved these Questions
Similar Questions
Consider the lines L1:r=a+λbandL2:r=b+μa, where a and b are non zero and non collinear vectors.
Statement-I L1andL2 are coplanar and the plane containing these lines passes through origin.
Statement-II (a−b)⋅(a×b)=0 and the plane containing L1andL2 is [r a b]=0 which passe through origin.View SolutionFind the value of x and y:ax+by=a−b
bx−ay=a+bView Solution
Knowledge Check
- Question 1 - Select One
The line y=kx+4 , where k is a constant, is graphed in the xy-plane. If the line contains the point (c, d) where c≠0 and d≠0, what is the slope of the line in terms of c and d ?
Ad−4cBc−4dC4−dcD4−cd - Question 2 - Select One
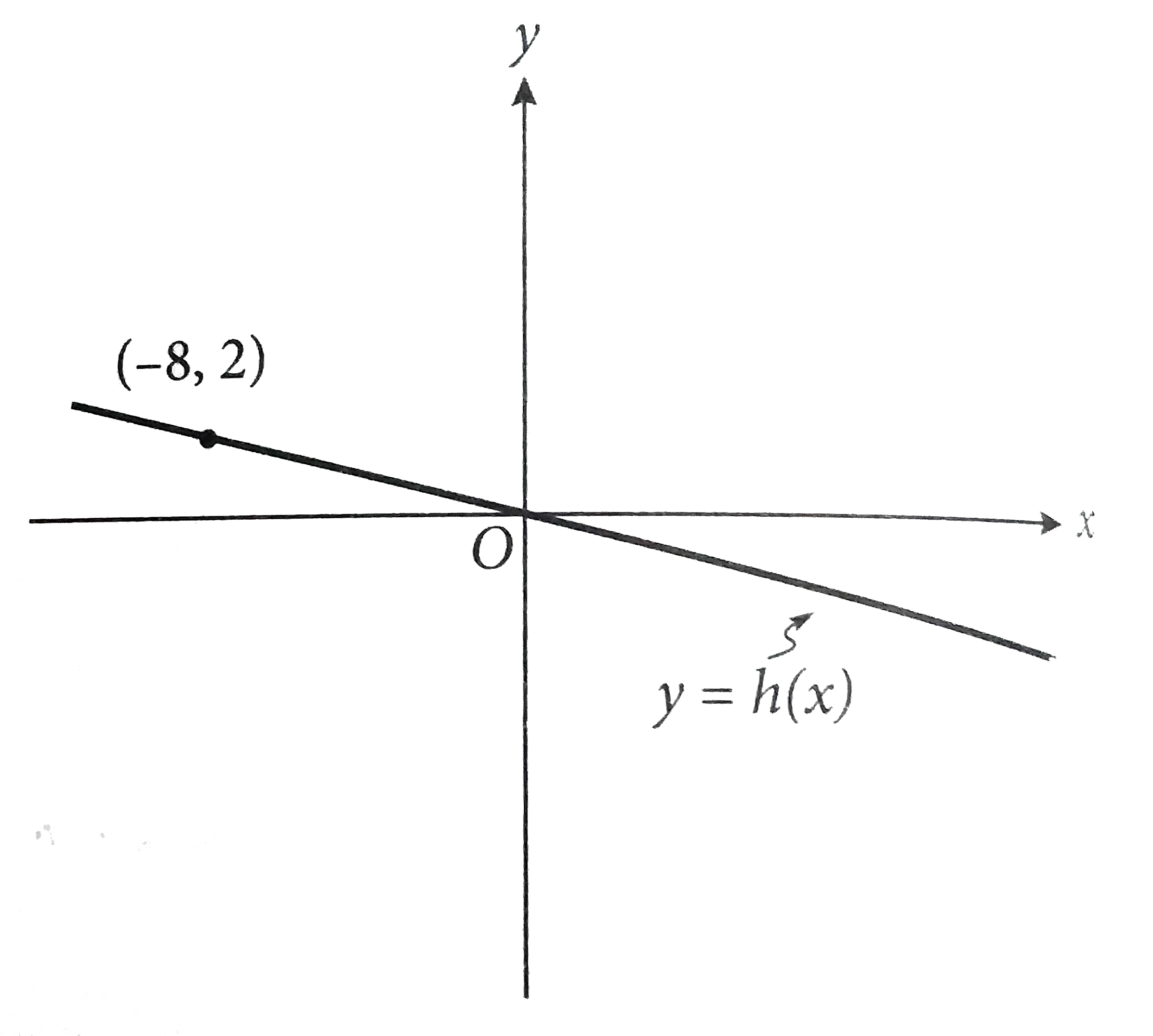
In the xy-plane above, a point (not shown) with coordinates (a,b) lies on the graph of the linear function h. IF a and b are non zero integers, what is the ratio of b to a?A−4→1B−2→1C−1→2D−1→4 - Question 3 - Select One
The graph of the linear function f has intercepts at (a,0) and (0, b) in the xy-plane. If a+b=0 and a≠b, which of the following is true about the slope of the graph of f ?
AIt is positive.BIt is negative.CIt equals zero.DIt is undefined.
If the line ax+by+c=0 is normal to the xy+5=0, then a and b have
View Solution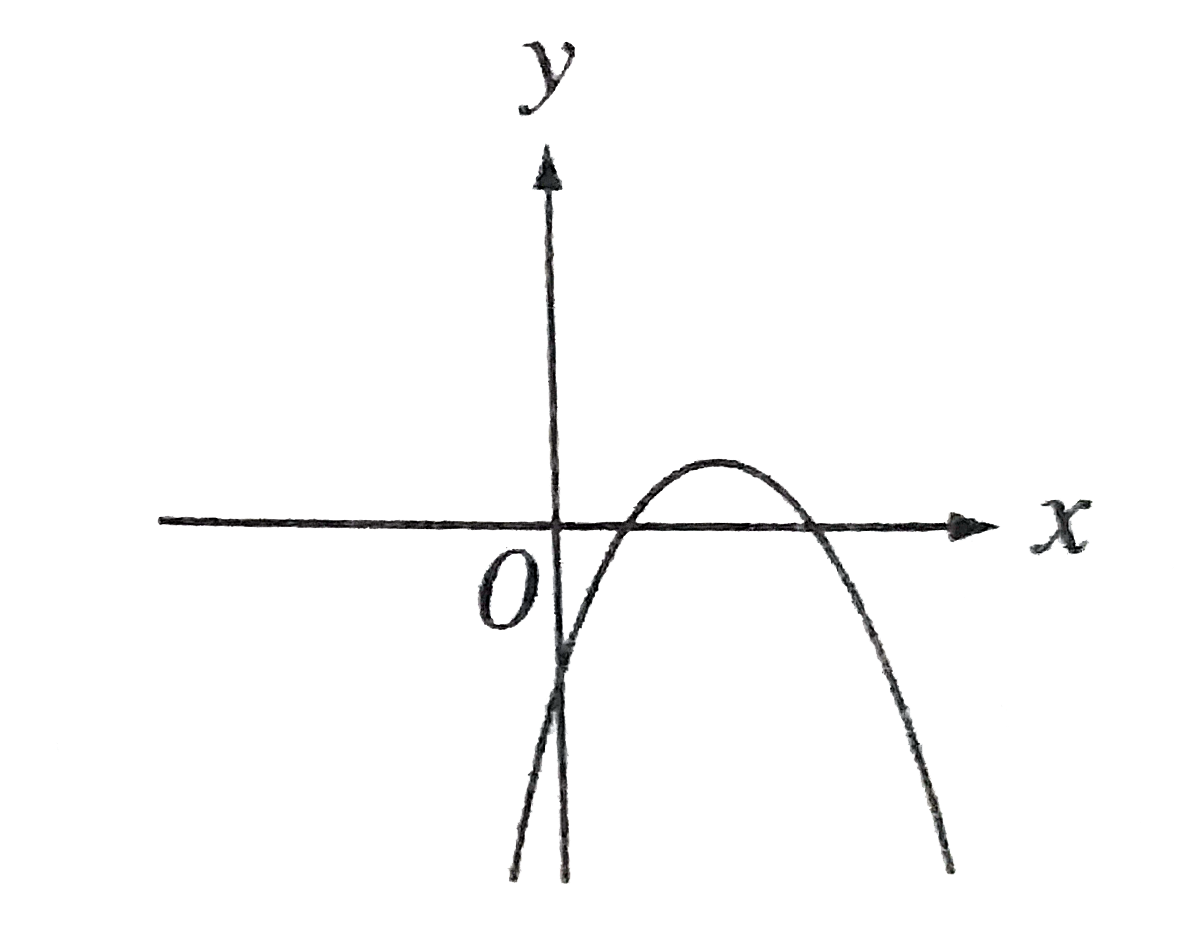
The graph of y=g(x) is shown in the figure above. If g(x)=ax2+bx+c for constants a,b and c and if abc≠0, then which of the following must be true?View Solution(ax+7)(bx−1)=12x2+kx+(b−13)
If the equation above is true for all values of x where a, b, and k are non-zero constants, what is the value of k?View SolutionIf a,h, and k are nonzero constants, and the parabola with equation y=a(x−h)2+k, in the xy-plane, passes through the point (h,5) and (0,2) , which of the following must be true ?
View Solutiony=−(x−3)2+a
In the equation above, a is a constant. The graph of the equation in the xy-plane is a parabola. Which of the following is true about the parabola?View Solution

