A cylinder rolls without slipping over a horizontal plane. The radius of the cylinder is equal to r. Find the curvature radii of trajectories traced out by the points A and B(see figure)

Let us draw the kinematic diagram of the rolling cylinder on the basis of the solution of problem 1.53.


As, an arbitrary point of the cylinder follows a curve, its normal acceleration and radius of curvature are related by the well known equation
wn=v2R
so, for point A, wA(n)=v2ARA
or, RA=4v2cω2r=4r (because vc=ωr, for pure rolling)
Similarly for point B,
wB(n)=v2BRB
ω2rcos45∘=(√2vc)2RB,
RB=2√2v2Cω2r=2√2r
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics59videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum82videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A cylinder rolls without slipping down an inclined plane, the number of degrees of freedom it has, is
A2B3C5D1 - Question 2 - Select One
A solid cylinder rolls without slipping down an inclined plane of height h. The velocity of the cylinder when it reaches the bouom is
A√2gh3B√4gh3C√3gh2D√gh - Question 3 - Select One
A solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
AMR22BMR2C32MR2D2MR2
If a solid cylinder rolls without slipping on an inclined plane of inclination 45°, then the minimum coefficient of friction required to support pure rolling is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45° then the minimum coefficient of friction required to support pure rolling is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination '0' then the minimum coefficient of friction required to support pure rolling is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45°, then the minimum coefficient of friction required to support pure rolling is
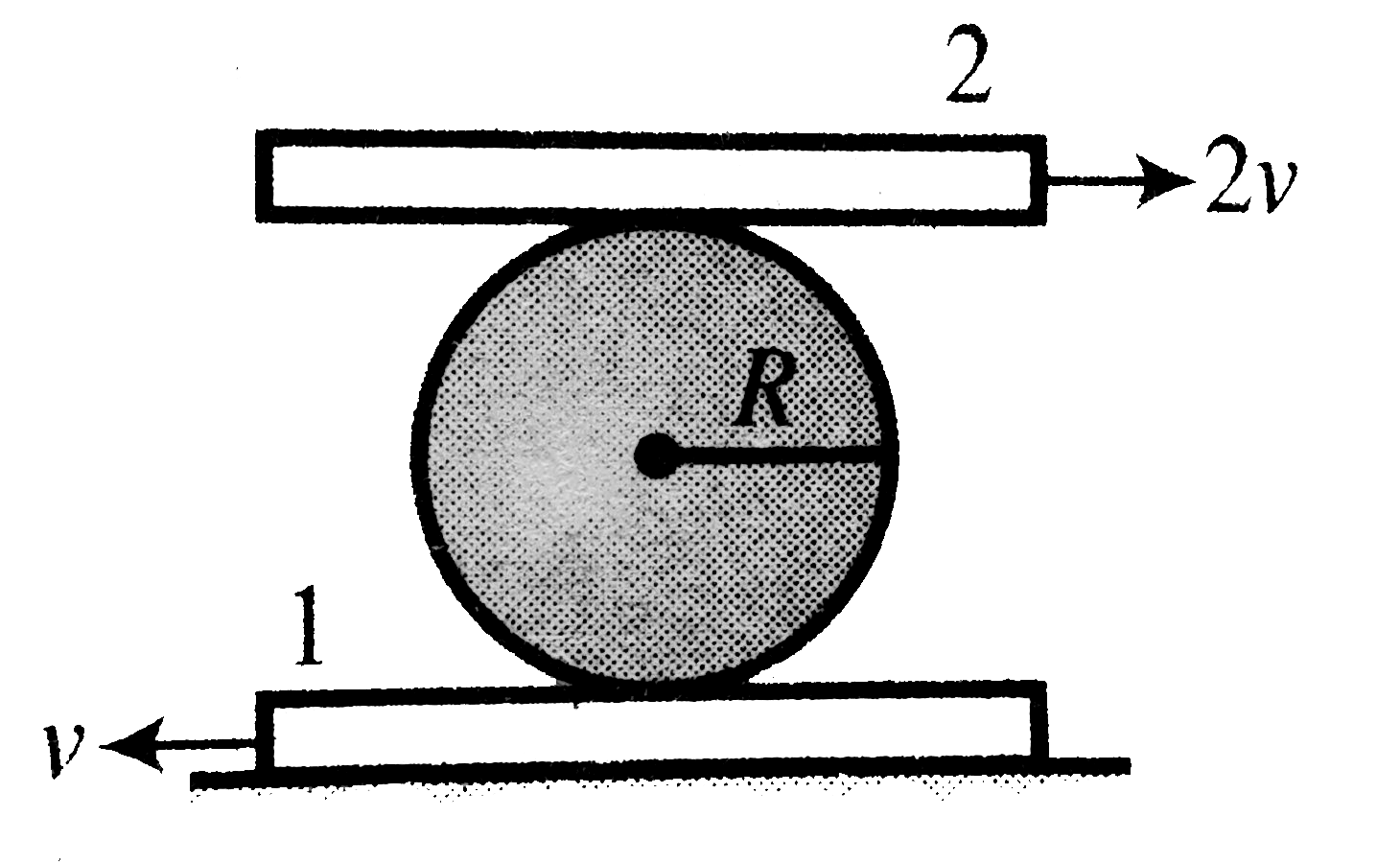
View SolutionA cylinder is rolling without sliding over two horizontal planks (surfaces) 1 and 2. If the velocities of the surfaces A and B are −vˆi and 2vˆi respectively, find the:
a. Position of instantaneous axis of rotation.
b. Angular velocity of the cylinder.
 View Solution
View Solution


