A block lying on a long horizontal conveyer belt moving at a constant velocity receives a velocity v0=5m/s relative to the ground in the direction opposite to the direction of motion of the conveyer. After t=4s, the velocity of the block becomes equal to the velocity of the belt. The coefficient of friction between the block and the belt is μ=0.2. Determine the velocity v of the conveyer belt.
To solve the problem step by step, we will analyze the motion of the block and the conveyor belt, taking into account the forces acting on the block due to friction.
Step 1: Understand the initial conditions
The block has an initial velocity v0=5m/s relative to the ground, moving in the opposite direction to the conveyor belt. Let the velocity of the conveyor belt be v (in the positive direction).
Step 2: Determine the acceleration due to friction
The frictional force acting on the block is given by:
Fs=μmg
where μ=0.2 is the coefficient of friction, m is the mass of the block, and g is the acceleration due to gravity (approximately 10m/s2).
The acceleration a of the block due to friction is:
a=Fsm=μg=0.2×10=2m/s2
Since the block is moving in the opposite direction to the conveyor belt, the acceleration will act in the direction opposite to the block's initial velocity, hence it will be negative:
a=−2m/s2
Step 3: Use the equation of motion
We can use the equation of motion to find the final velocity vf of the block after time t=4s:
vf=v0+at
Substituting the known values:
vf=5+(−2)(4)=5−8=−3m/s
The negative sign indicates that the final velocity of the block is in the opposite direction to the positive direction of the conveyor belt.
Step 4: Relate the final velocity of the block to the conveyor belt
At t=4s, the block's velocity becomes equal to that of the conveyor belt:
vf=v
From our previous calculation, we have:
−3=v
Thus, the velocity of the conveyor belt is:
v=3m/s (in the positive direction)
Final Answer
The velocity of the conveyor belt is v=3m/s.
---
The block has an initial velocity v0=5m/s relative to the ground, moving in the opposite direction to the conveyor belt. Let the velocity of the conveyor belt be v (in the positive direction).
The frictional force acting on the block is given by:
Fs=μmg
where μ=0.2 is the coefficient of friction, m is the mass of the block, and g is the acceleration due to gravity (approximately 10m/s2).
a=Fsm=μg=0.2×10=2m/s2
Since the block is moving in the opposite direction to the conveyor belt, the acceleration will act in the direction opposite to the block's initial velocity, hence it will be negative:
a=−2m/s2
We can use the equation of motion to find the final velocity vf of the block after time t=4s:
vf=v0+at
Substituting the known values:
vf=5+(−2)(4)=5−8=−3m/s
The negative sign indicates that the final velocity of the block is in the opposite direction to the positive direction of the conveyor belt.
At t=4s, the block's velocity becomes equal to that of the conveyor belt:
vf=v
From our previous calculation, we have:
−3=v
Thus, the velocity of the conveyor belt is:
v=3m/s (in the positive direction)
The velocity of the conveyor belt is v=3m/s.
Topper's Solved these Questions
Similar Questions
Find out the distance travelled by the block on incline before it stops. Initial velocity of the block is 10 m/s and coefficient of friction between the block and incline is μ=0.5.
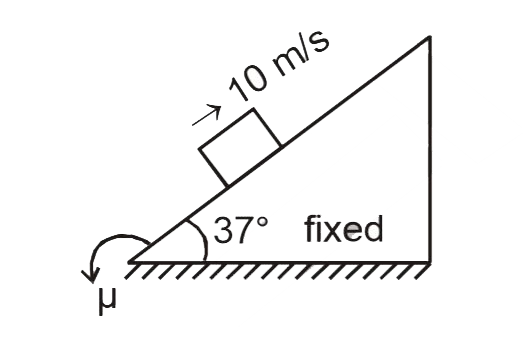 View Solution
View SolutionA horizontal conveyor belt moves with a constant velocity V.A small block is projected with a velocity of 6m/s on it in a direction opposite to the direction of motion of the belt The block comes to rest relative to the belt in a time 4s.μ=0.3,g=10.m/s2 Find V .
View Solution
Knowledge Check
- Question 1 - Select One
A block is gently placed on a conveyor belt moving horizontal with constant speed After t=4s the velocity of the block becomes equal to velocity of the belt If the coefficient of friction between the block and the belt is μ=0.2, then the velocity of the conveyor belt is .
A8/sB6m/sC4m/sD2m/s - Question 2 - Select One
Block B moves to the right with a constant velocity v0. The velocity of body A relative to B is
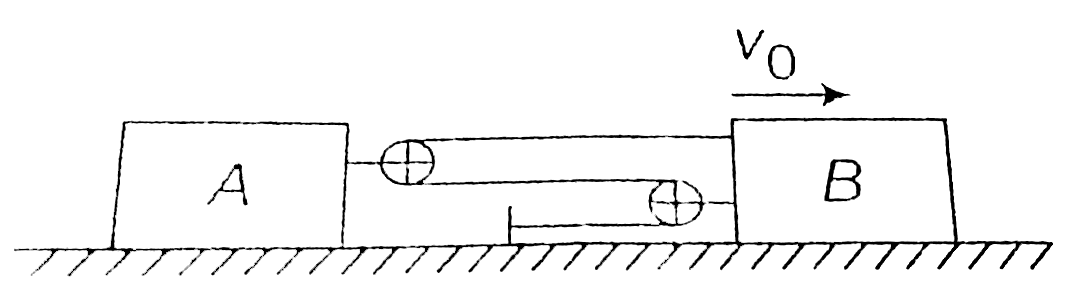 Av02, towards leftBv02, towards rightC3v02, towards leftD3v02, towards right
Av02, towards leftBv02, towards rightC3v02, towards leftD3v02, towards right - Question 3 - Select One
In the block moves up with constant velocity v m//s. Find F
 AF=mg2BF=2mg3CF=mg3DF=m3
AF=mg2BF=2mg3CF=mg3DF=m3
Block B moves to the right with a constant velocity v0. The velocity of body A relative to B is :
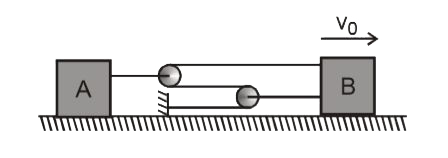 View Solution
View SolutionA long piece of paper is being pulled on a horizontal surface with a constant velocity υ along its length. Width of the paper is L. A small block moving horizontally, perpendicular to the direction of motion of the paper, with velocity v slides onto the paper. The coefficient of friction between the block and the paper is μ. Find maximum value of v such that the block does not cross the opposite edge of the paper.
 View Solution
View SolutionA rectangular block is kept on a rough horizontal surface and given some initial velocity. The coefficient of friction between the block and the surface is constant. The block will topple
View SolutionA block of mass m slides 0n a frictionless table. It is constrained to move inside a ring of radius R . At time t=0 , block is moving along the inside of the ring (i.e. in the tangential direction) with velocity v0 . The coefficient of friction between the block and the ring is μ . Find the speed of the block at time t .
 View Solution
View SolutionBlock of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
 View Solution
View Solution

