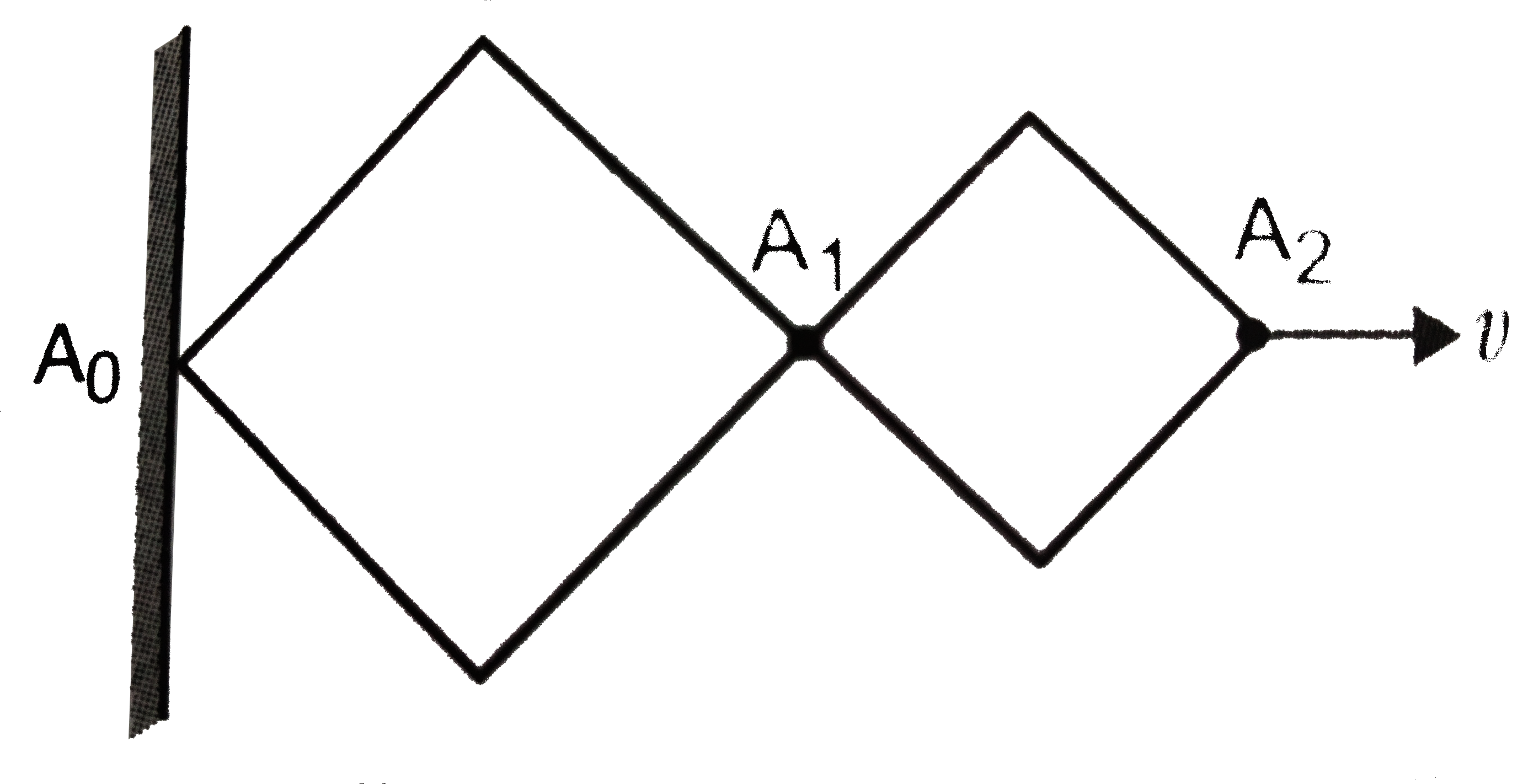
A hinged construction consists of three rhombs with the ratio of sides

Three blocks A, B, and C of masses $3 M, 2 M$ , and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is $a_{1}, a_{2}$ and $a_{3}$ , respectively, then

The value of acceleration $a_{1}$ at the moment string RS is cut is
Ag, downward
Bg, upward
CMore than g, downwards
DZero
The angular velocities of three bodies in $S H M$ are $ω_{1}, ω_{2}, ω_{3}$ with their respective amplitudes as $A_{1}, A_{2}, A_{3}$ . If all three bodies have same mass and maximum velocity then
A $A_{1} ω_{1} = A_{2} ω_{2} = A_{3} ω_{3}$
B $A_{1} ω_{1}^{2} = A_{2} ω_{2}^{2} = A_{3} ω_{3}^{2}$
C $A_{1}^{2} ω_{1} = A_{2}^{2} ω_{2} = A_{2}^{2} ω_{2}$
D $A_{1}^{2} ω_{1}^{2} = A_{2}^{2} ω_{2}^{2} = A_{3}^{2} ω_{3}^{2}$
In the arrangement shown above, all surfaces are frictionless. The rod R is constrained to move vertically. The vertically acceleration of R is $a_{1}$ and the horizontal accelration of the wedge W is $a_{2}$ . The ratio $a_{1} / a_{2}$ is equal to
A $tan α$
B $cot α$
C $sin α$
D $cos α$

A hinged construction consists of three rhombs with the ratio of sides 3 : 2 : 1

(Fig). Vertex $A_{3}$ moves in the horizontal direction at a velocity v. Determine the velocities of vertices $A_{1}, A_{2}$ and $B_{2}$ at the instant when the angles of the construction are $90^{\circ}$