A light spring of length l and rigidity k is placed vertically on a table. A small ball of mass m falls on it. Determine the height h from the surface of the tube at which the ball will have the maximum velocity.
To solve the problem, we need to determine the height h from the surface of the table at which the ball will have the maximum velocity as it falls onto the spring. Here’s a step-by-step solution:
Step 1: Understand the Forces Acting on the Ball
When the ball of mass m falls, it is acted upon by two forces:
- The gravitational force mg acting downward.
- The spring force kx acting upward when the spring is compressed by a distance x.
Step 2: Determine the Condition for Maximum Velocity
The ball will continue to accelerate downward until the spring force equals the gravitational force. The maximum velocity will occur just before the spring starts to decelerate the ball. This happens when:
mg=kx
Where x is the compression of the spring.
Step 3: Relate Compression to Height
The height from which the ball falls can be expressed in terms of the spring's compression:
- Let L be the original length of the spring.
- The height h from the table surface when the spring is compressed by x is given by:
h=L−x
Step 4: Substitute for x
From the equilibrium condition mg=kx, we can express x as:
x=mgk
Step 5: Substitute x into the Height Equation
Now, substituting x back into the height equation:
h=L−mgk
Step 6: Final Expression for Height
Thus, the height h from the surface of the table at which the ball will have the maximum velocity is:
h=L−mgk
Conclusion
The height h from the surface of the table at which the ball will have the maximum velocity is given by:
h=L−mgk
When the ball of mass m falls, it is acted upon by two forces:
- The gravitational force mg acting downward.
- The spring force kx acting upward when the spring is compressed by a distance x.
The ball will continue to accelerate downward until the spring force equals the gravitational force. The maximum velocity will occur just before the spring starts to decelerate the ball. This happens when:
mg=kx
Where x is the compression of the spring.
The height from which the ball falls can be expressed in terms of the spring's compression:
- Let L be the original length of the spring.
- The height h from the table surface when the spring is compressed by x is given by:
h=L−x
From the equilibrium condition mg=kx, we can express x as:
x=mgk
Now, substituting x back into the height equation:
h=L−mgk
Thus, the height h from the surface of the table at which the ball will have the maximum velocity is:
h=L−mgk
The height h from the surface of the table at which the ball will have the maximum velocity is given by:
h=L−mgk
Topper's Solved these Questions
Similar Questions
A ball of mass m is attached to a light string of length L and suspended vertically. A constant horizontal force, whose magnitude F equals the weight of the ball, is applied Determine the speed of the ball as it reaches the 90∘ level.
View Solution.A ball is projected upwards from a height h above the surface of the earth with velocity v .The time at which the ball strikes the ground is
View Solution
Knowledge Check
A massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
Ag√mkBg√2mkCg2√mkDg√m2kA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
Avg+2hg√2Bvg[1−√1+2hg]Cvg[1+√1+2ghv2]Dvg[1+√v2+2hh]A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
Amg(h+d)+12kd2Bmg(h+d)−12kd2Cmg(h−d)−12kd2Dmg(h−d)+12kd2
A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
View SolutionA small iron ball falls from rest through a large height h into a water column, the final velocity
View SolutionA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
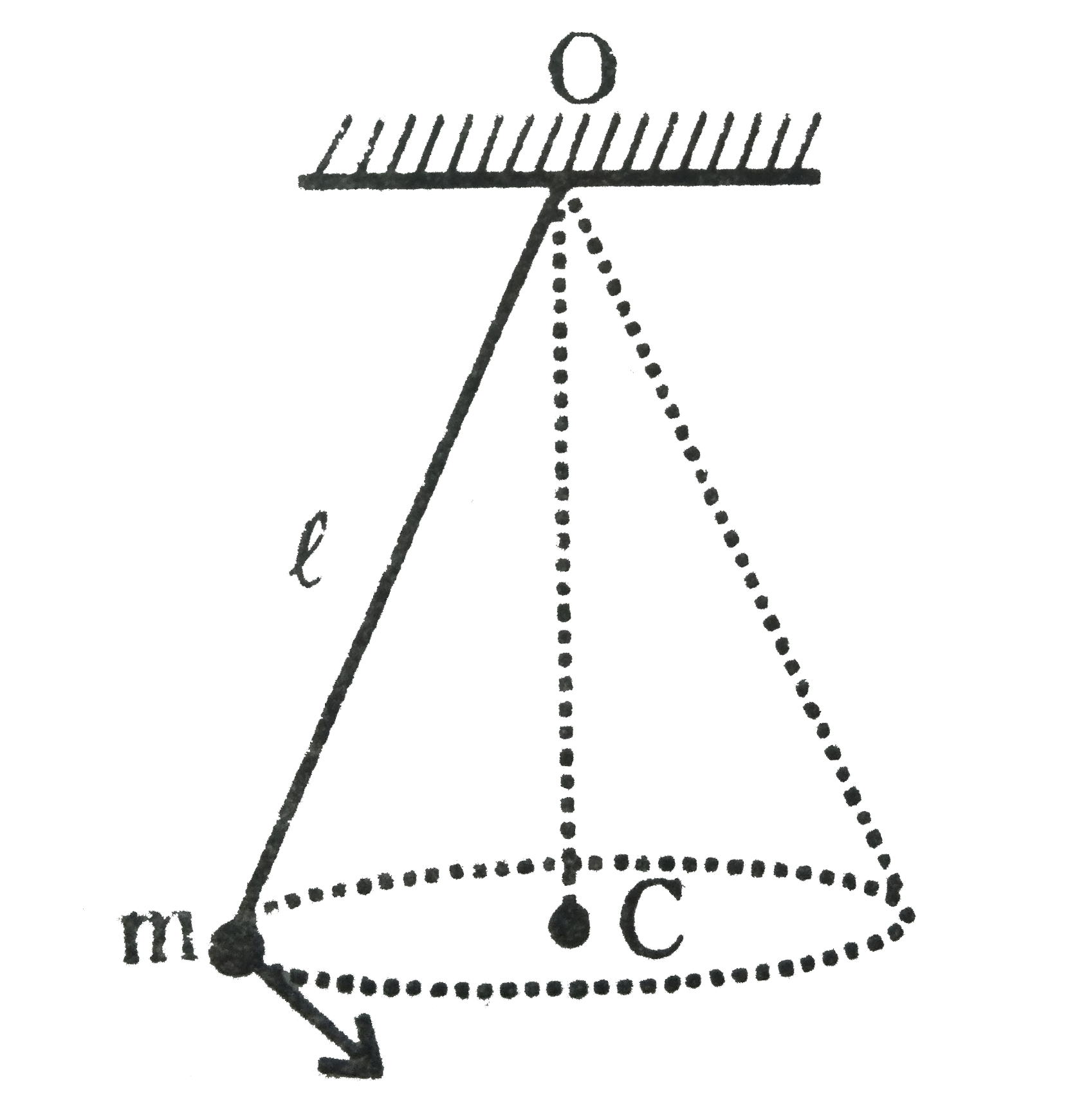 .
.
View SolutionA ball of mass m suspended from a rigid support by an inextensible massless string is released from a height h above its lowest point. At its lowest point it collides elastically with a block of mass 2m at rest on a frictionless surface. Neglect the dimensions of the ball and the block. After the collision the ball rises to a maximum height of–

View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
View Solution
