An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
m0
m
m2
m−1
The correct Answer is:A
To solve the problem, we will use the principle of conservation of energy. Here's a step-by-step breakdown of the solution:
Step 1: Identify the Initial and Final States
- The object of mass m is released from rest at the top of the inclined plane (point A) with height h.
- At the bottom of the inclined plane (point B), the object will have a certain speed V.
Step 2: Write the Energy Conservation Equation
According to the conservation of mechanical energy:
Potential Energy at A+Kinetic Energy at A=Potential Energy at B+Kinetic Energy at B
Step 3: Calculate the Energies
- At point A (top of the incline):
- Potential Energy (PE) = mgh
- Kinetic Energy (KE) = 0 (since the object is at rest)
- At point B (bottom of the incline):
- Potential Energy (PE) = 0 (height is zero)
- Kinetic Energy (KE) = 12mV2
Step 4: Set Up the Equation
Substituting the values into the energy conservation equation:
mgh+0=0+12mV2
This simplifies to:
mgh=12mV2
Step 5: Simplify the Equation
- We can cancel m from both sides (assuming m≠0):
gh=12V2
Step 6: Solve for V
Rearranging the equation to solve for V:
V2=2gh
Taking the square root of both sides gives:
V=√2gh
Step 7: Analyze the Proportionality
- The expression V=√2gh shows that the speed V is dependent on g (acceleration due to gravity) and h (height).
- Importantly, there is no dependence on the mass m. Thus, the speed V is independent of the mass of the object.
Conclusion
Since the speed V does not depend on m, we can conclude that:
V∝m0
Thus, the answer is m0.
---
- The object of mass m is released from rest at the top of the inclined plane (point A) with height h.
- At the bottom of the inclined plane (point B), the object will have a certain speed V.
According to the conservation of mechanical energy:
Potential Energy at A+Kinetic Energy at A=Potential Energy at B+Kinetic Energy at B
- At point A (top of the incline):
- Potential Energy (PE) = mgh
- Kinetic Energy (KE) = 0 (since the object is at rest)
- Potential Energy (PE) = 0 (height is zero)
- Kinetic Energy (KE) = 12mV2
Substituting the values into the energy conservation equation:
mgh+0=0+12mV2
This simplifies to:
mgh=12mV2
- We can cancel m from both sides (assuming m≠0):
gh=12V2
Rearranging the equation to solve for V:
V2=2gh
Taking the square root of both sides gives:
V=√2gh
- The expression V=√2gh shows that the speed V is dependent on g (acceleration due to gravity) and h (height).
- Importantly, there is no dependence on the mass m. Thus, the speed V is independent of the mass of the object.
Since the speed V does not depend on m, we can conclude that:
V∝m0
Thus, the answer is m0.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT18videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON15videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason15videos
WAVES
Similar Questions
An object of mass m is allowed to fall from rest along a rough inclined plane. The speed of the object on reaching the bottom of the plane is proportional to:
View SolutionA spherical object of mass m and radius R is released from the top of a smooth inclined plane of height h and angle of inclination is 37° . The radius of gyration of the object is K. The speed of object at the bottom of inclined plane is
View Solution
Knowledge Check
- Question 1 - Select One
A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle θ2 reaches the bottom in time t2 If the two inclined planes have the same height, the relation between t1andt2 is
At2t1=(sinθ1sinθ2)1/2Bt2t1=1Ct2t1=sinθ1sinθ2Dt2t1=sin2θ1sin2θ2
A block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10m/s at the bottom of the inclined then work done by the friction force on the block will be
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
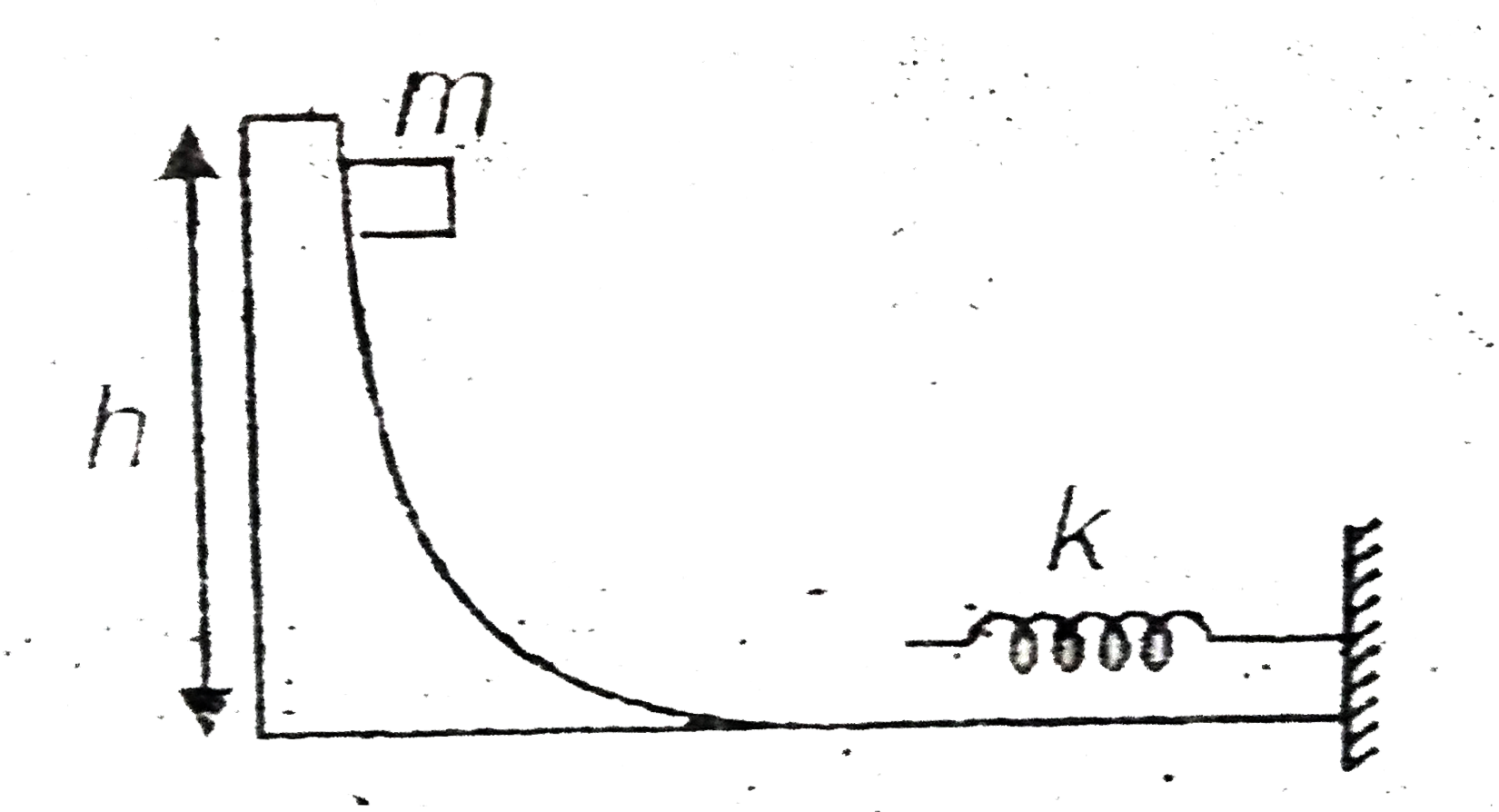 View Solution
View Solution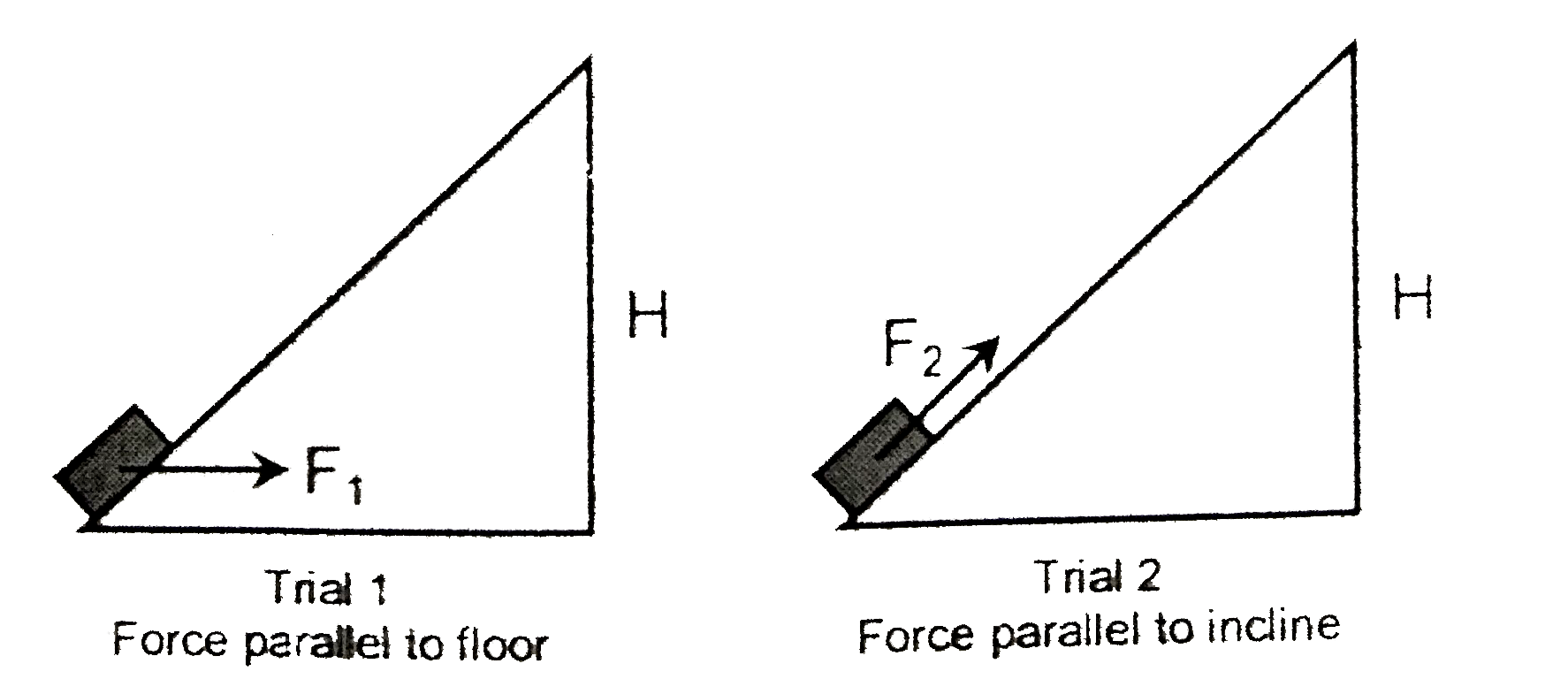
An object of mass M starts from rest at the bottom of a fixed incline of height H. A person decides to push the object up the incline in one of two ways with an applied force shown in the diagram. In each of the trials, the object reaches the top of the incline with speed V. How would the work done by the person on the block compare for the two trials? Assume the same constant non-zero coefficient of kinetic friction between the incline and the object for both trials.View SolutionSTATEMENT-1: A ball of mass m is released from the top of a smooth inclined plane. At the same time another ball of same mass allowed to fall freely from same height. When both balls reaches the bottom of the plane, momentum will not be equal
because
STATEMENT-2: Momentum depends on the direction of velocity as well as its magnitude.View SolutionA block released from rest from the tope of a smooth inclined plane of angle of inclination θ1=30∘ reaches the bottom in time t1. The same block, released from rest from the top of another smooth inclined plane of angle of inclination θ2=45∘ reaches the bottom in time t2. Time t1 and t2 are related as ( Assume that the initial heights of blocks in the two cases are equal ).
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
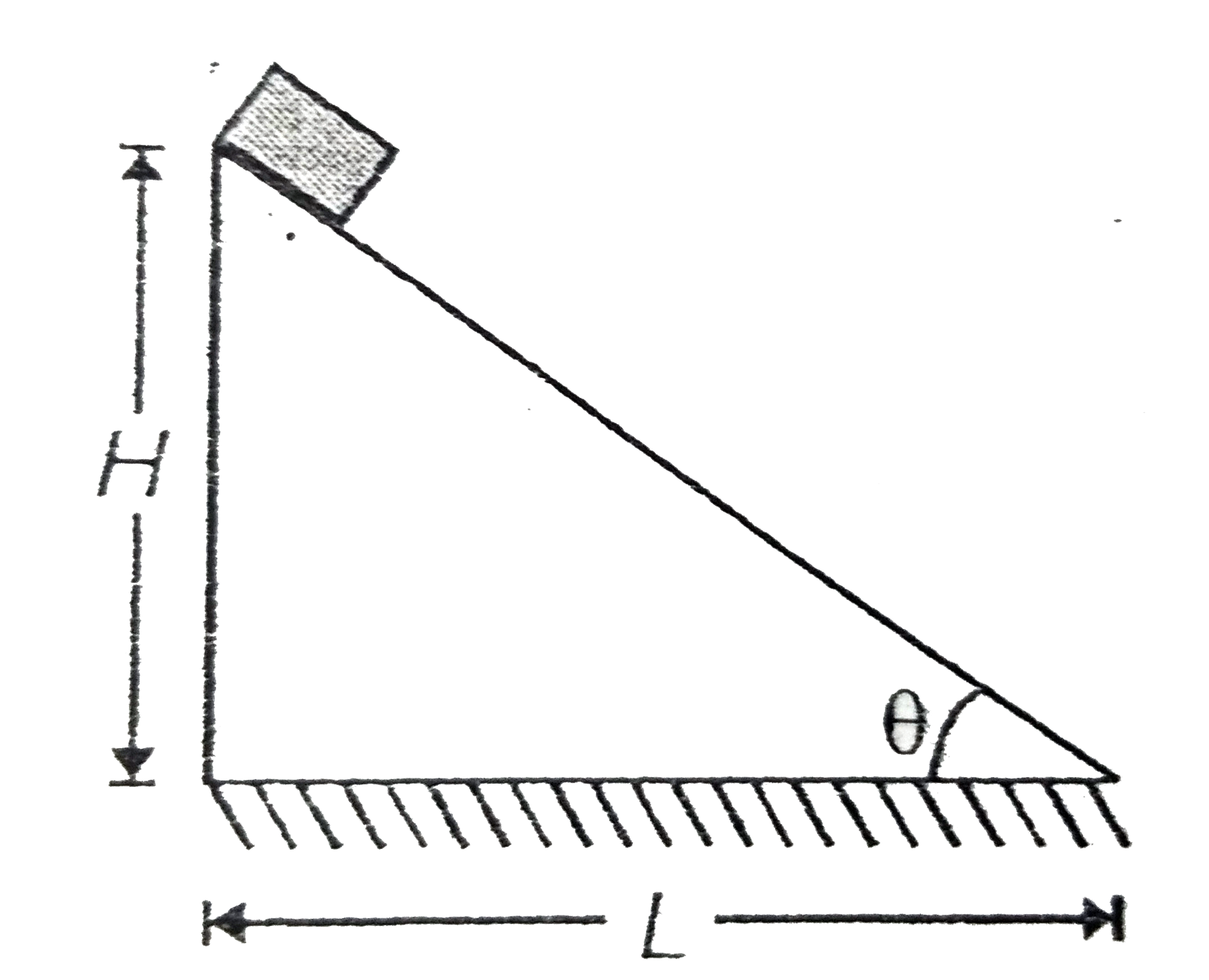 View Solution
View Solution

