There is uniformly charged disc of surface charge density σ and of radius 1m. H=10m height below the disc is a gun which is continuously emitting a charged particle and its isotopic in the vertically upward direction. The particles are charged through same potential before being emitted. The charge of the particle is q=8×10−19C. The difference of potential energies of particle and the isotopic at B is 10−23Joule. Also the velocity of the particle at B is zero. The ratio of masses of particle and isotopic is 32. If the total energy of isotope at B is 1.1k×10−23J Then find k..(Given σ/ε0=10−4N/C).
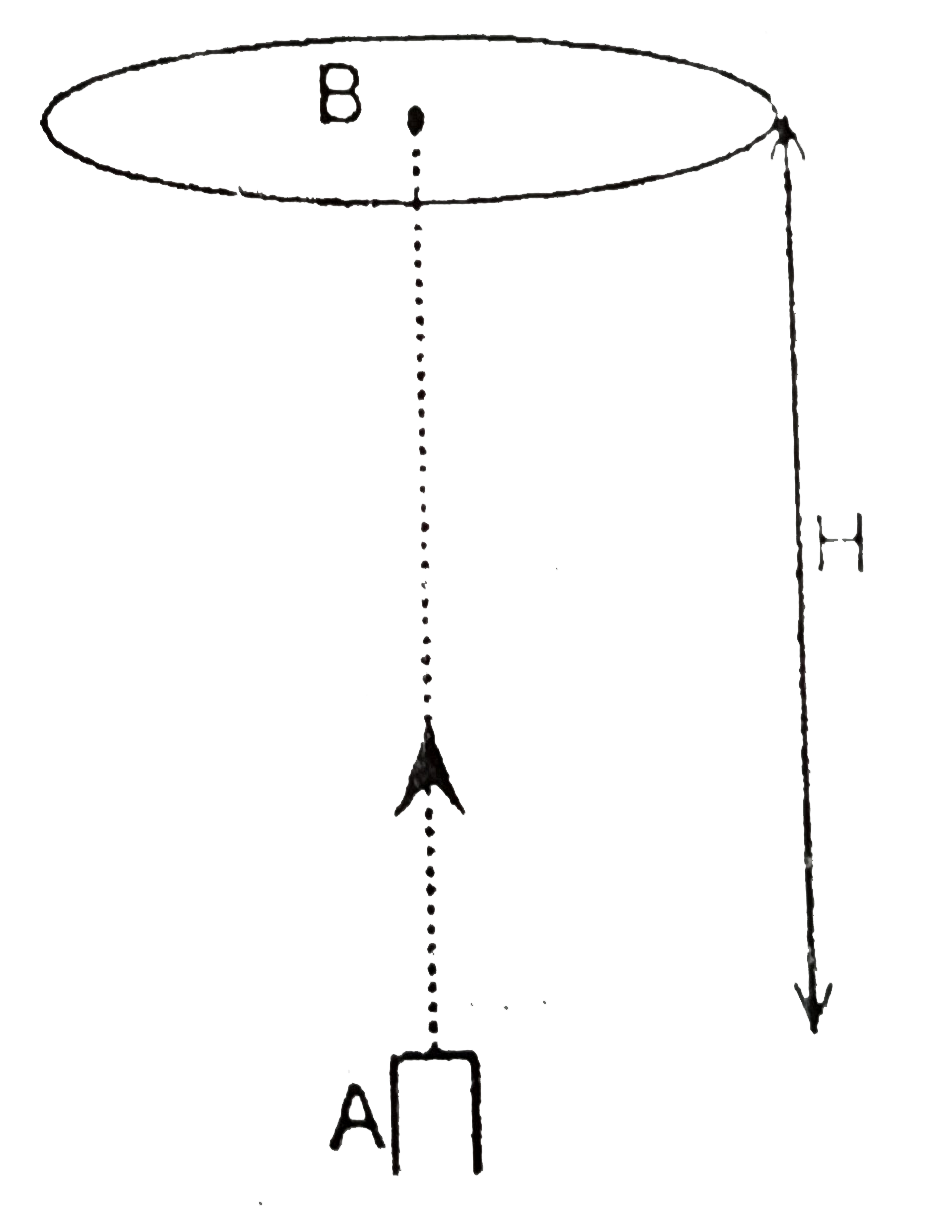
At 'A' Total energy of particle
EPA=12mPV2PA+qφ+0
And of isotope
EiA=12m1V2PA+qφ+0⇒EPA=EiA
At B, ϕB=σa2ε0
Energy of particle is
EPB=12mP×0+qverϕa+mPgh
Energy of istope EiB=12miV2iB+qφB+migh
(mr−mi)gh=10−23
mP=1.5×10−25kg.
mr=0.5×10−25kg.
∴EPB=EiB
12miV2B=(mP−mi)gh=10−23
EiB=10−23+8×0−19×0.5×10−4+10−252×10×10
=5.5×10−23J.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
AmvQB2Q√mVC√2mQVD√2QVm - Question 2 - Select One
The electric field that can balance a charged particle of mass 3.2×10−27kg is (Given that the charge on the particle is 1.6×10−19C)
A19.6×10−8NC−1B20×10−6NC−1C19.6×108NC−1D20×106NC−1 - Question 3 - Select One
The specific charge of a proton is 9.6×107C kg−1.
The specific charge of an alpha particle will beA9.6×107C kg−1B19.2×107C kg−1C4.8×107C kg−1D2.4×107C kg−1
Positively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View SolutionA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
View SolutionA charged particle is moving in a magnetic field of strength B perpendicular to the direction of the field. If q and m denote the charge and mass of the particle respectively, then the frequency of rotation of the particle is
View SolutionA positively charged disc is placed on a horizontal plane. A charged particle is released from a certain height on its axis. The particle just reaches the centre of the disc. Select the correct alternative.
View SolutionA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle E, then frequency of rotation is
View Solution

