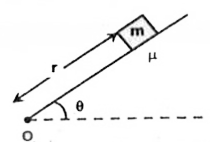
A small block of mass m is placed at a distance r from one end of a plank. The plank is given a constant angular velocity about an axis passing through point O and perpendicular to the plane. The block starts sliding down the plane when the plank makes an angle with horizontal. Calculate the coefficient of friction between the particle and the plank.
The correct Answer is:
Step by step video, text & image solution for A small block of mass m is placed at a distance r from one end of a plank. The plank is given a constant angular velocity omega about an axis passing through point O and perpendicular to the plane. The block starts sliding down the plane when the plank makes an angle theta with horizontal. Calculate the coefficient of friction between the particle and the plank. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (Level-II & III)18videos
LAWS OF MOTION
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) (Level - 1)50videos
LAWS OF MOTION
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (Level-I)(True/False)2videos
LAWS OF MOTION
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE5videos
KINEMATICS
- BOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type2videos
MAGNETIC
Similar Questions
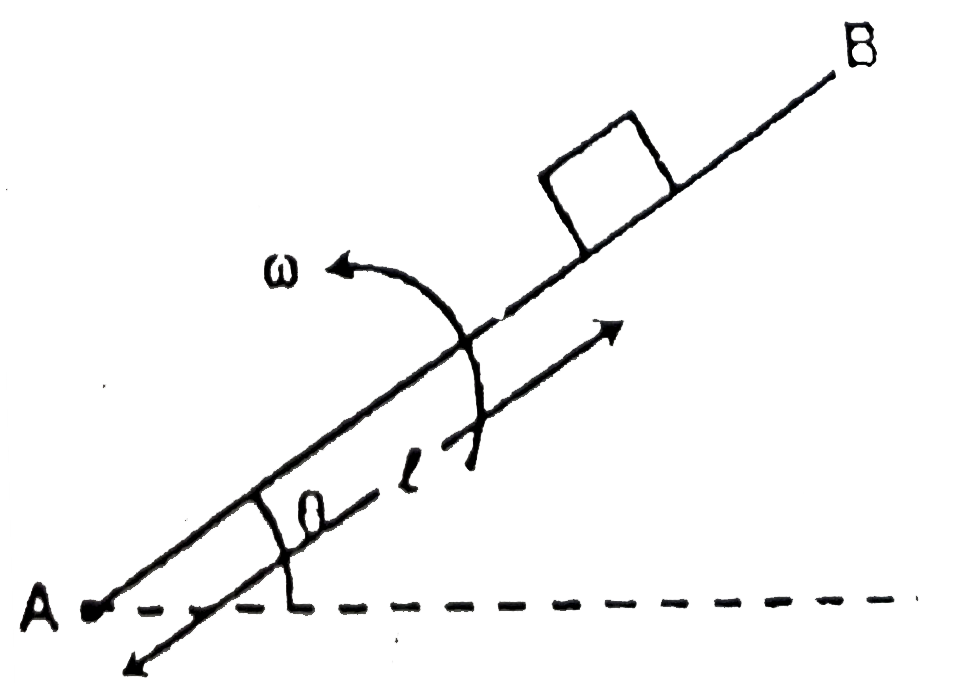
A plank is rotating in a vertical plane about one of its ends with a constant angular velocity ω=√2rad/s. A block of mass m=2kg is placed at a distance l=1m from its end A (see figure) which is hinged. The block starts sliding down when the plank makes an angle θ=30∘ with the horizontal. If coefficient of friction between the plank and the block is μ and given that μ2=k/25. Find the value of k.
 View Solution
View SolutionA solid sphere of mass M is placed on the top of a plank of the same mass, after giving an angular velocity ω0 at t=0. Find the velocity of the plank and the sphere when the sphere starts rolling:,
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1Dμmgθ - Question 2 - Select One
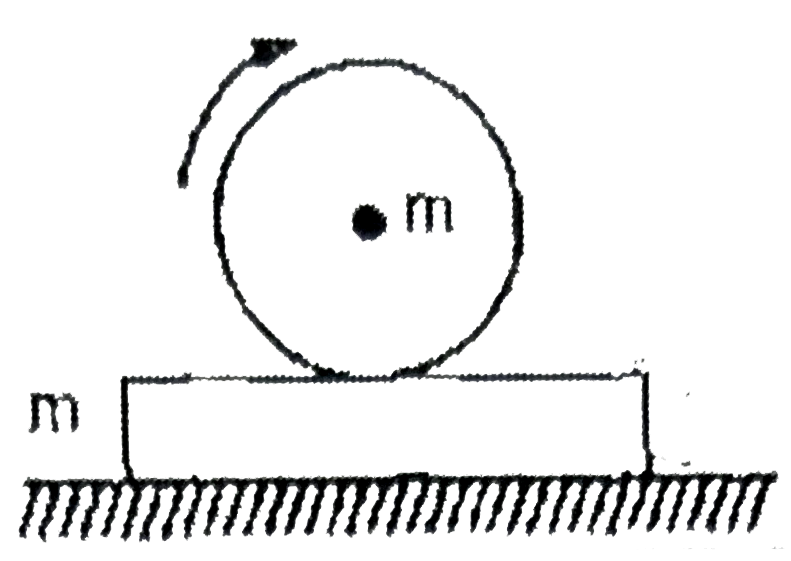
A sphere of mass m is given some angular velocity about a horizontal axis through the center, and gently placed on a plank of mass m. The coefficient of friction between the two is μ. The plank rests on a smooth horizontal surface. The intial acceleration of the sphere relative to the plank will be:
 AzeroBμgC75μgD2μg
AzeroBμgC75μgD2μg - Question 3 - Select One
A sphere of mass m is given some angular velocity about a horizontal axis through its centre and gently placed on a plank of mass 'm'. The co-efficent of friction between the two is μ. The plank rests on a smooth horizontal surface. The initial acceleration of the centre of sphere relative to the plank will be
 AzeroBμgC(7/5)μgD2μg
AzeroBμgC(7/5)μgD2μg
A box of mass 4 kg is placed on a wooden plank of length 1.5m which is lying on the ground. The plank is lifted from one end along its length so that it becomes inclined. It is noted that when the vertical height of the top end of the plank from the ground becomes 0.5m, the box begins to slide. Find the coefficient of friction between the box and the plank.
View SolutionA wooden plank OA rotates in vertical plane about horizontal axis through O with a constant angular velocity ω=3rad/s . As it passes the position θ=0 , a small mass m is placed upon it at a radial distance r=0⋅5 m . If the mass m starts sliding at θ=37∘ , find the coefficient of friction between mass and the plane .
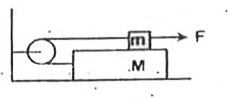
View SolutionA small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?View SolutionA plank of mass M and length L is placed at rest on a smooth horizontal surface. A small block of mass m is projected with a velocity v0 from the left end of it as shown in figure. The coefficient of friction between the block and the plank is m, and its value is such that the block becomes stationary with respect to the plank before it reaches the other end.

a. Find the time and common velocity when relative sliding between the block and the plank stops.
b. Find the work done by the friction force on the block during the period it slides on the plank. Is the work positive or negative?
c. Calculate the work done on the plank during the same period. Is the work positive or negative?
d. Also, determine the net work done by friction, Is it positive or negative?View SolutionTwo men A and B are sitting at th eend of a plank of length L, if plank is rotating with angular velocity ω about an axis perpendicular to its length and passing through a point at a distance of L/3 from A. The angular velocity of B with respect to A is
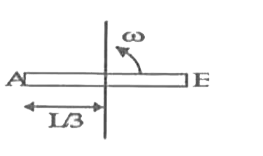 View Solution
View Solution

