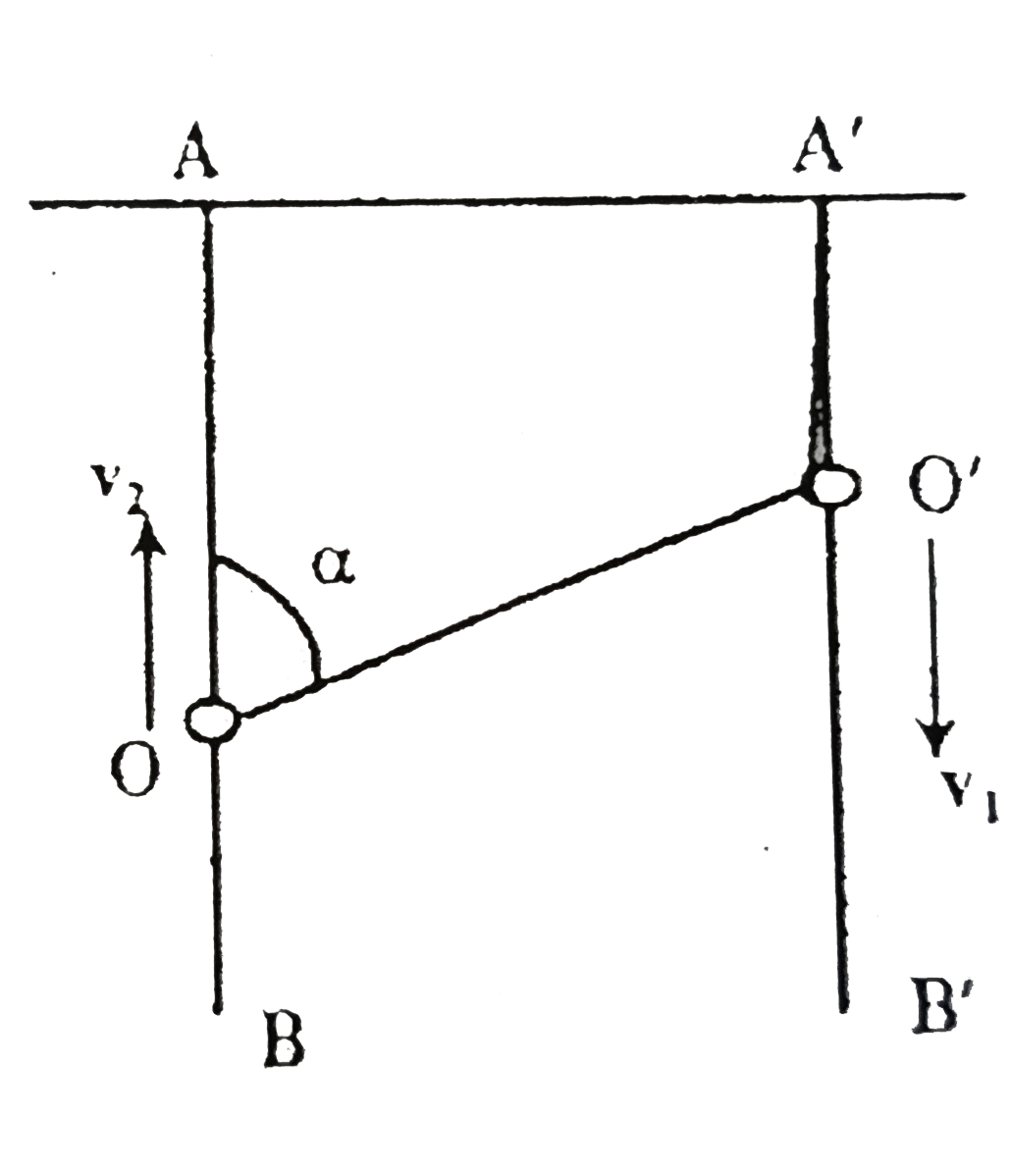
Two small rings O and O' are put on two vertical stationery rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O.
Assuming that ring O' moves downwards at a constant velocity v1, determine the velocity v2 of the ring O, when ∠AOO'=α.
v1[2sin2α/2cosα]
v1[2cos2α/2sinα]
v1[3cos2α/2sinα]
None of these
v2cosα+v1cosα=v1
⇒v2=v1[2sin2(α/2)cosα]
Topper's Solved these Questions
Similar Questions
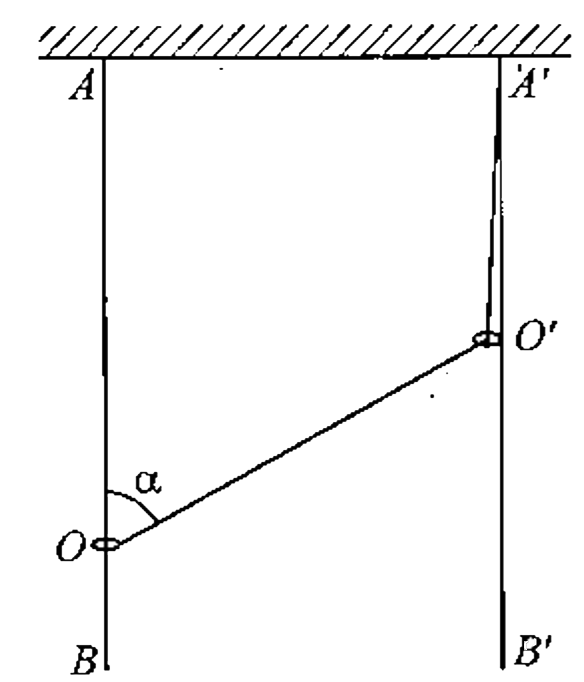
Two rings O and O' are put on two vertical stationary rods AB and A'B' respectively as shown in figure. An inextensible string is fixed at point A' and on ring O and is passed through O' moves downwards at a constant speed v, find the velocity of the ring O in terms of α.
 View Solution
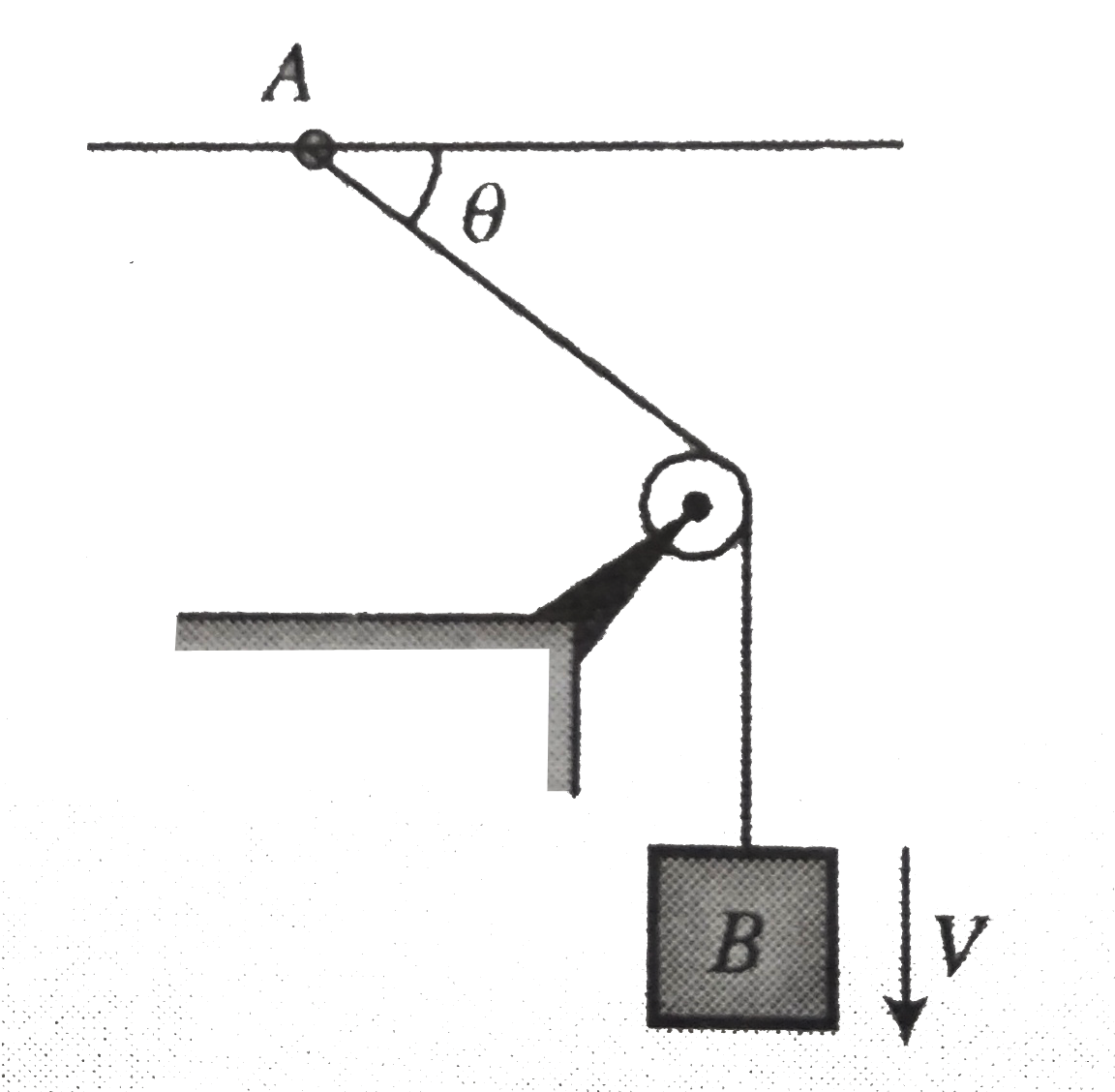
View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two small rings O and O' are put on two vertical stationary rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O. Assuming that ring O' moves downwards at a constant velocity v1, then velocity v2 of the ring O, when ∠AOO'=α is
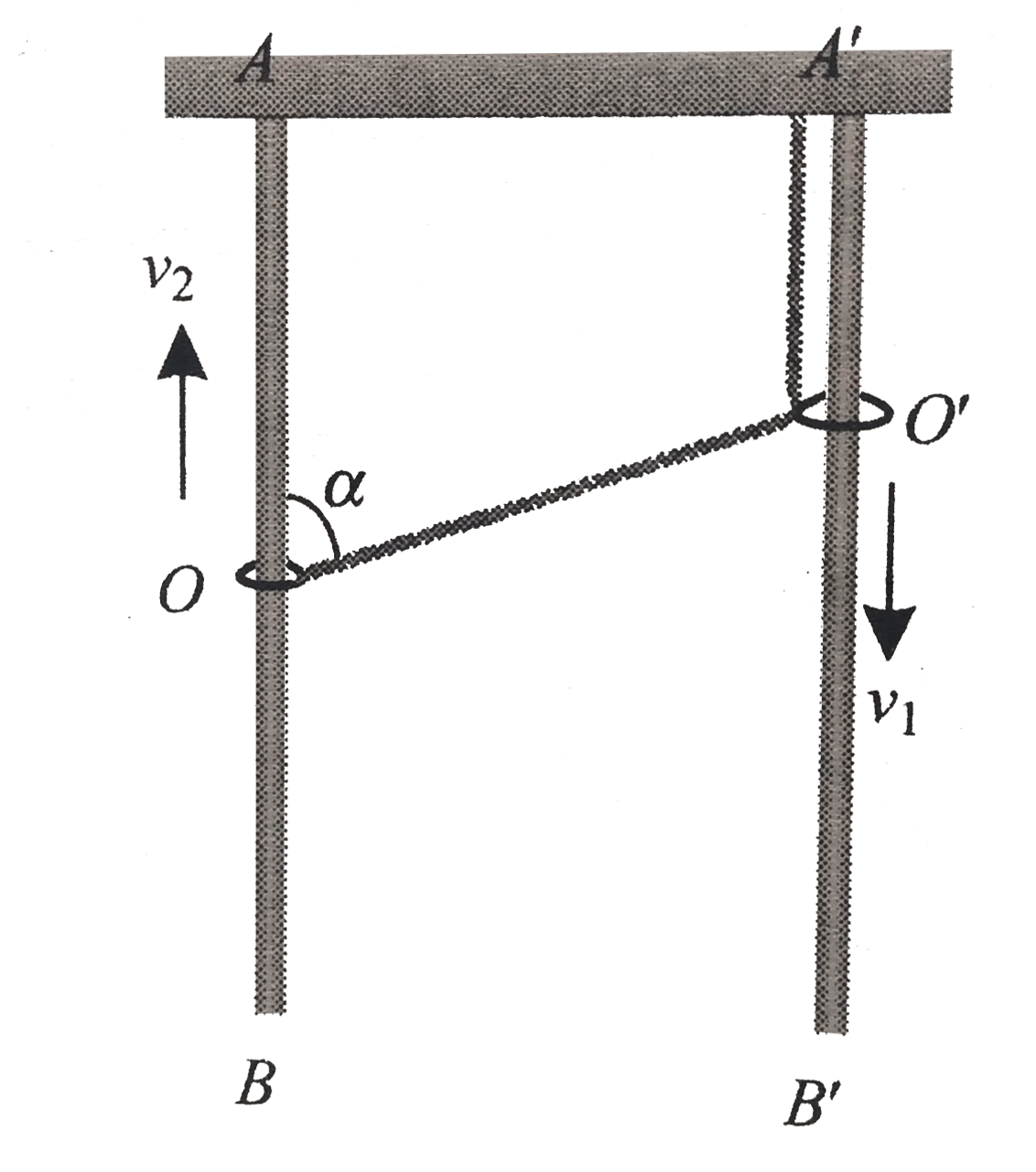 Av1[2sin2α/2cosα]Bv1[2sin2α/2sinα]Cv1[3sin2α/2sinα]DNone of these
Av1[2sin2α/2cosα]Bv1[2sin2α/2sinα]Cv1[3sin2α/2sinα]DNone of these - Question 2 - Select One
A particle is moving in a straight line and passes through a point O with a velocity of 6ms−1 The particle moves with a constant retardation of 2ms−2 for 4 s and there after moves with constant velocity. How long after leaving O does the particle return to O
A√2tB(2+√2)tCt√2DCan not perdicted unless accelerationis given - Question 3 - Select One
The moment of inertia of a uniform rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. Then I1/I2 is
Aπ23B2π23C4π23D8π23
A smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
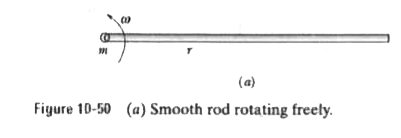 View Solution
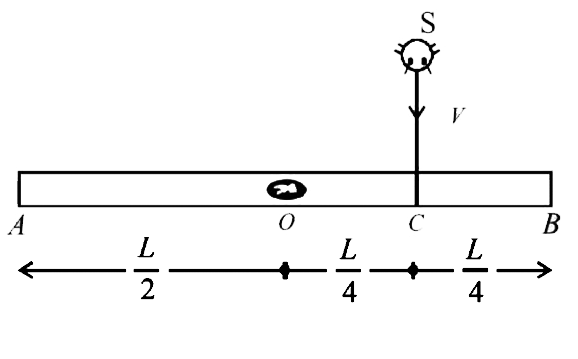
View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
 View Solution
View SolutionAn isotropic point source kept at 'O' produces intensity l0 at point A. find the mean energy flow rate through a ring centred at A and having its plane perpendicular to the line OA. The distance OA is x arid radius of ring is R.
View SolutionA uniform conducting wire is used to make a ring and its two diameters AB and CD. The ring is placed in a uniform magnetic field B perpendicular to its plane. The resistance of the wire per unit length is λΩ/m.
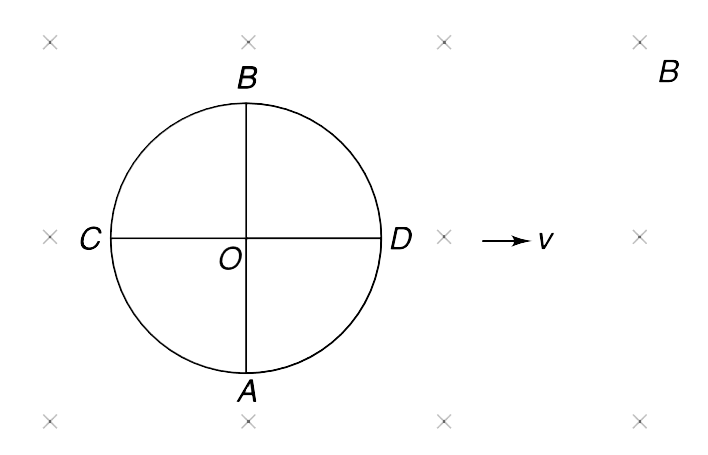
(a) Find the current in BO and BC when the ring is moved with constant velocity v in its plane.
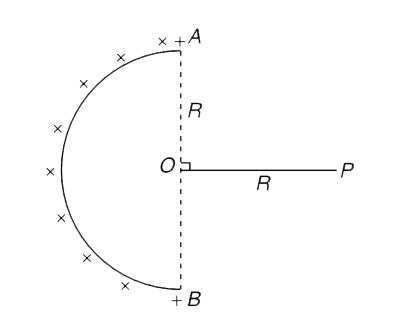
(b) Find current in BO and BC when the ring is kept stationary but the magnetic field is increased at a constant rate of dBDt=αT/s. Assume that magnetic field is confined inside the circular ring only. Take radius of the ring to be a.View SolutionA sermicircular ring of radius R carries a uniform linear charge of λ. P is a point in the plane of the ring at a distance R from centre O. OP is perpendicular to AB. Find electric field intensity at point P.
 View Solution
View Solution

