Two identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

F2m
F−kxm
F−2kxm
kxm
Equation of motion of A :
kx=ma⇒a=kxm
For B:F−T=ma'
⇒a'=F−kxm
⇒ The relative acceleration =ar=|a'−a|=F−2kxm

Topper's Solved these Questions
Similar Questions
Two identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
View SolutionDeduce the relations for (a) particle velocity (b) particle acceleration
View Solution
Knowledge Check
Two identical particle each of mass m are inter connects by a light spring of stiffness k ,the time period for small oscillation is equal to
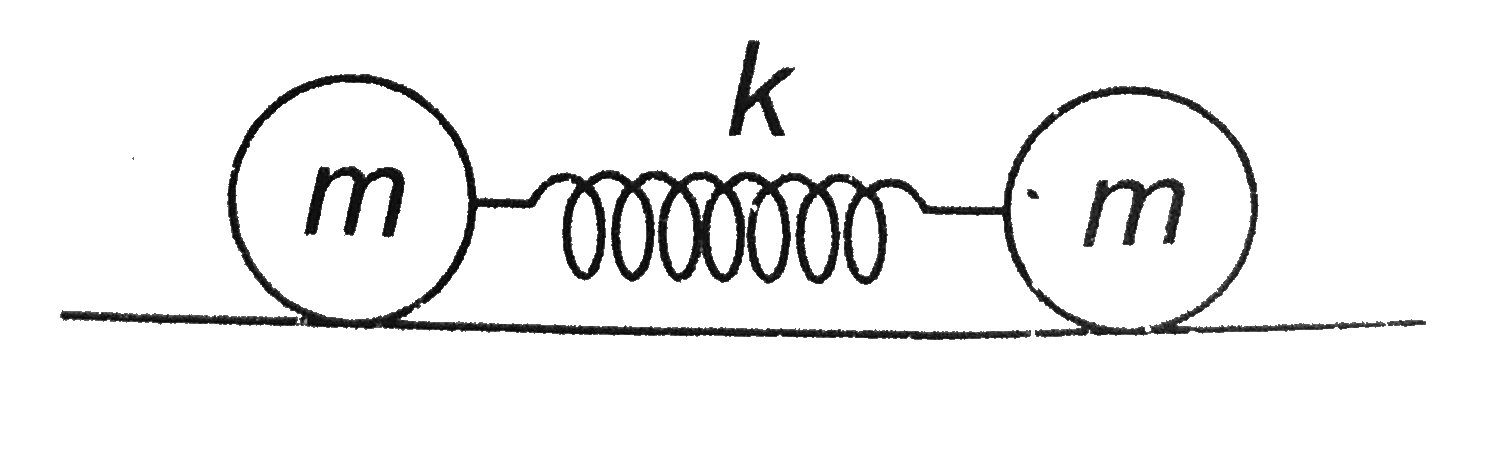 A2π√mkBπ2√mkCπ√m2kDπ√2mk
A2π√mkBπ2√mkCπ√m2kDπ√2mkTwo identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
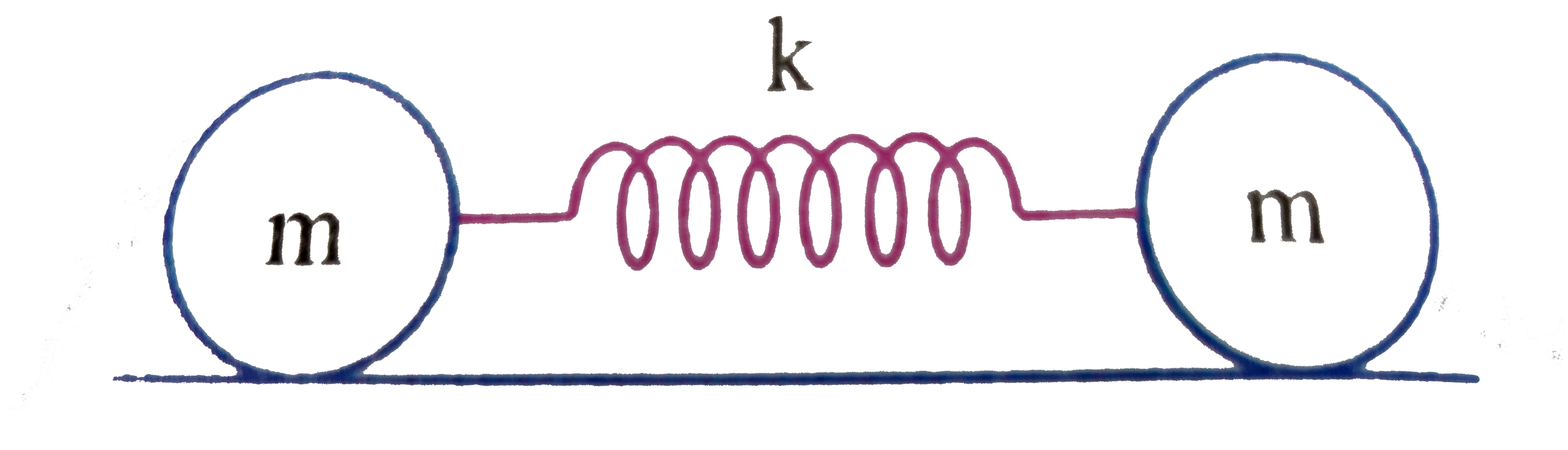 Aπ5√2Bπ10√2sCπ5sDπ10s
Aπ5√2Bπ10√2sCπ5sDπ10sTwo particles A and B each of mass m are kept stationary by applying a horizontal force F=mg on particle B as show in figure .Then
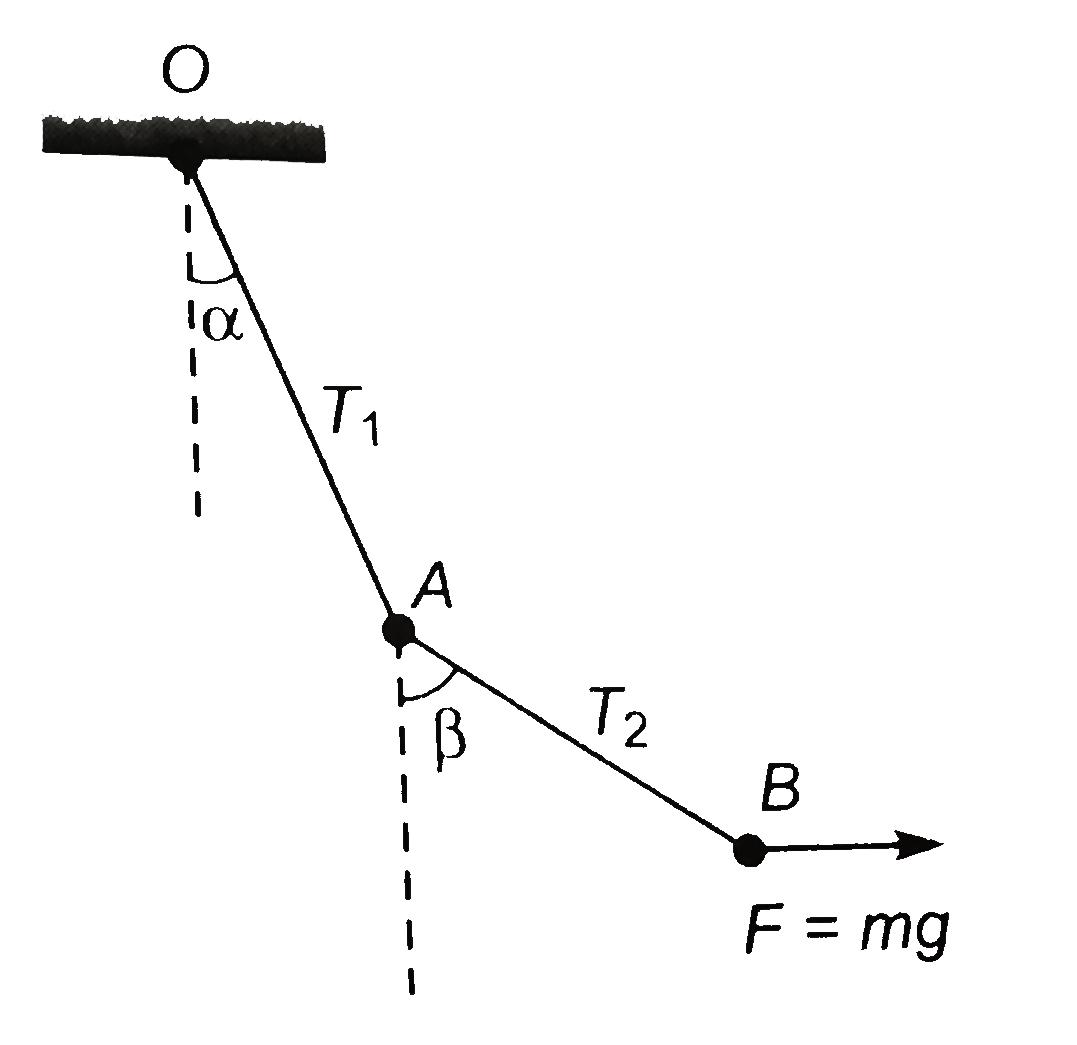 A2tanβ=tanαB2T1=5T2CT1√2=T2√5DNone of these
A2tanβ=tanαB2T1=5T2CT1√2=T2√5DNone of these
In an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionThree particles A,B and C each of mass m are lying at the corners of an equilateral triangle of side L . If the particle A is released keeping the particles B and C fixed , the magnitude of instantaneous acceleration of A is
View SolutionTwo bodies A and B each of mass M are fixed together by a massless spring A force F acts on the mass B as shown in fig At the instant shown the mass A has acceleration a. What is the acceleration of mass B?

View SolutionA particle of mass M and radius of gyration K is rotating with angular acceleration α. The torque acting on the particle is
View SolutionA particle of mass M and radius of gyration K is rotating with angular acceleration α. The torque acting on the particle is
View Solution
