A particle m starts with zero velocity along a line y=4d. The position of particle m varies as x=Asinωt, At ωt=π/2, its angular momentum with respect to the origin
mAωd
mωd/A
mAd/ω
zero
At ωt=π/2
u=Aωcost=0
So, angular momentum of particle m with respect to the origin should be zero.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Position of a particle varies as y=cos2ωt−sin2ωt. It is
Aharmonic but not SHMBSHM with period (πω)CSHM with period (2πω)Dperiodic with period (πω) but not SHM. - Question 2 - Select One
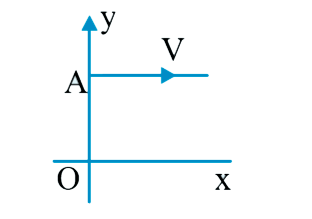
A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
AzeroBremains constantCgoes on increasingDgoes on decreasing - Question 3 - Select One
A body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
Ais zeroBremains constantCgoes on increasingDgoes on decreasing
A body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Calculate its angular momentum with respect to the origin?
 View Solution
View SolutionA particle performs uniform circular velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
View SolutionA point particle travels in a straight line at constant speed. The closest it comes to the origin of coordinatesisa distance l With respect to this origin, does the particle have nonzero angular momentum ? As the particle moves along its straight line path, does its angular momentum with respect to origin change.
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionA xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is
 View Solution
View Solution

