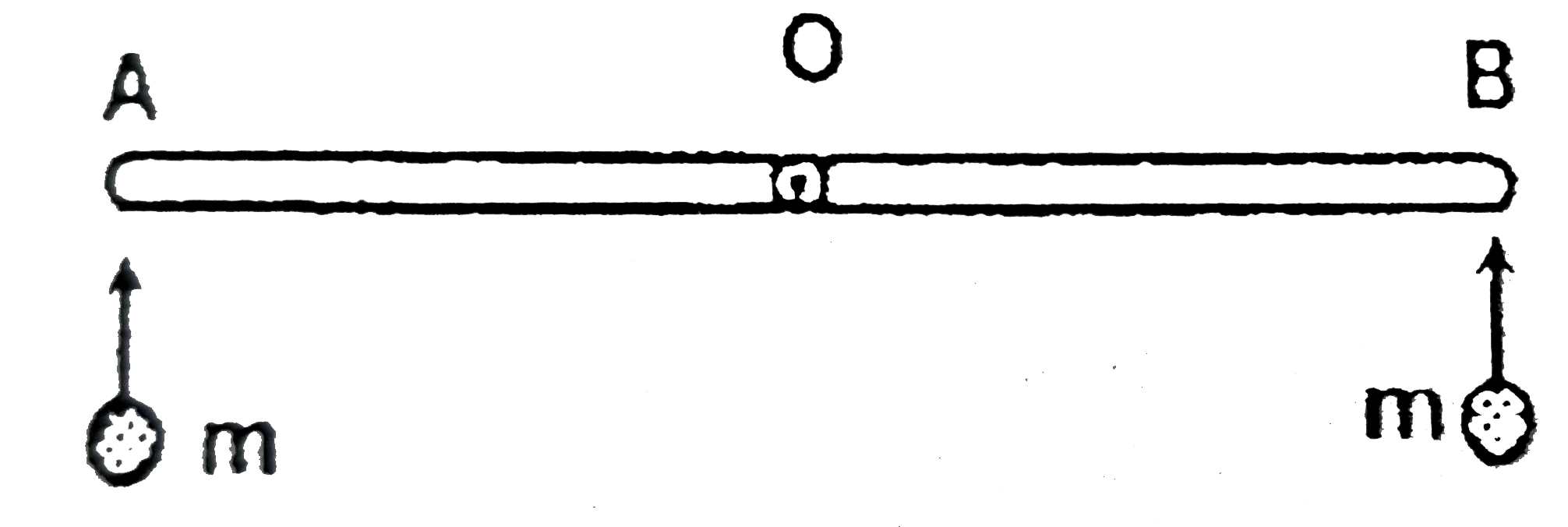
Two identical unifrom rods OA and OB each of length l and mass m are c

Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rod of length L. They are placed on a frictionless horizontal surface. Another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown in the figure. If the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will be

A $\frac{4}{3} \frac{u}{l}$
B $\frac{u}{l}$
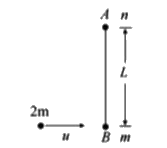C $\frac{2}{3} \frac{u}{l}$
Dnone of these
A ball of mass m moving with a speed $u_{0}$ collides elastically with a rod of mass M suspended in the vertical plane by the hinge O. The rod is free to rotate in the vertical plane. Before and after the collision.

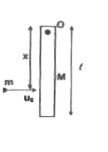ALinear momentum of the ball and rod system is conserved
BLinear momentum of the ball and rod system is conserved only when the collision is elastic
CLinear momentum of the ball and rod system may be conserved for a particular value of x.
Dnone of these
Two particles of masses $m_{1}$ and $m_{2}$ are connected to a rigid massless rod of length r to constitute a dumb bell which is free to move in the plane. The moment of inertia of the dumb bell about an axis perpendicular to the plane passing through the centre of mass is
A $\frac{m_{1} m_{2} r^{2}}{m_{1} + m_{2}}$
B $(m_{1} + m_{2}) r^{2}$
C $\frac{m_{1} m_{2} r^{2}}{m_{1} - m_{2}}$
D $(m_{1} - m_{2}) r^{2}$

A ball of mass m moving with a speed $u_{0}$ collides elastically with a rod of mass M suspended in the vertical plane by the hinge O. The rod is free to rotate in the vertical plane. Before and after the collision.