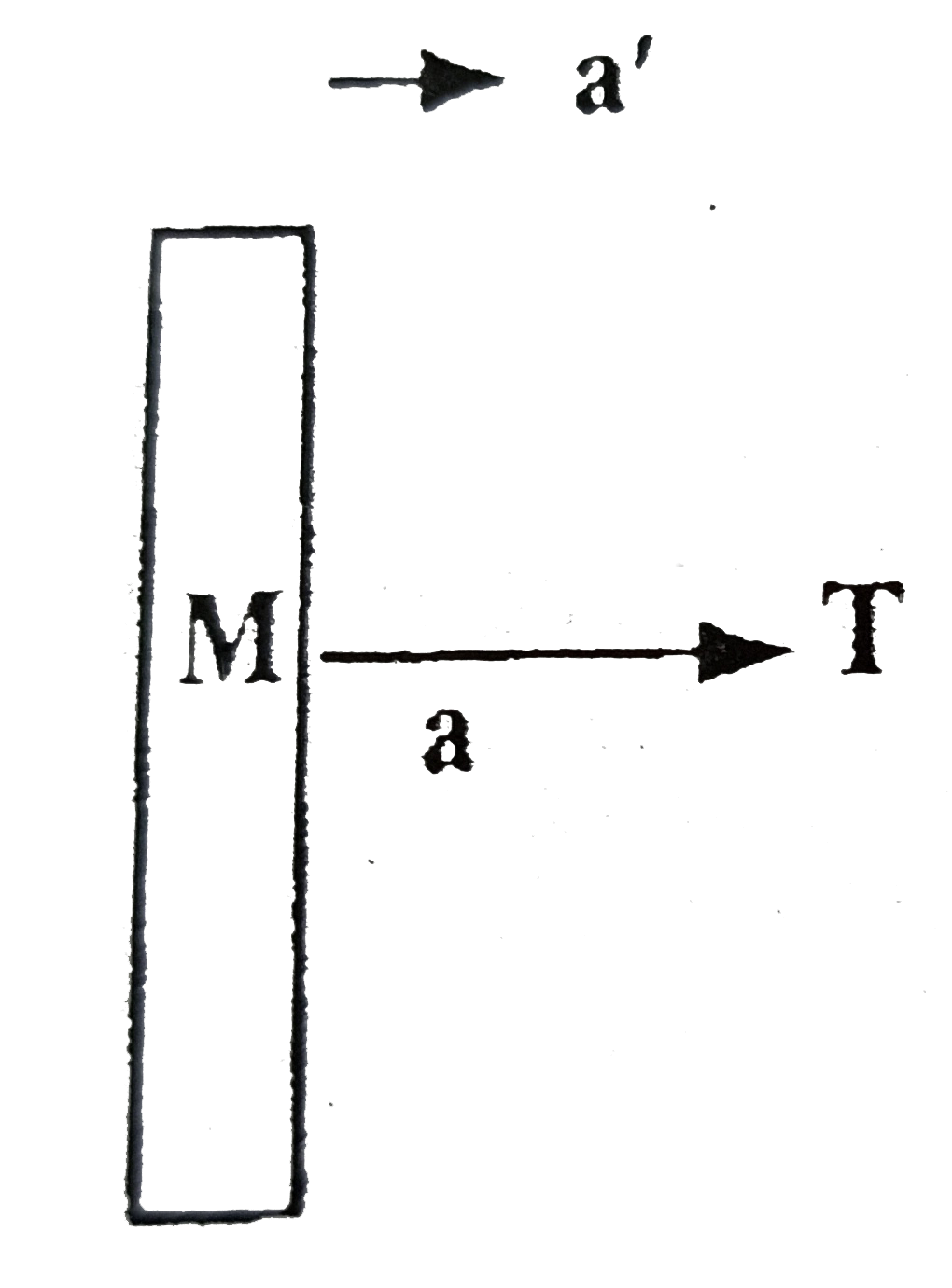
A spool of thread of mass m and moment of inertia I is attached to the block of mass M. Along a horizontal line passing through the centre of the spool, a constant force F is applied as shown. The surface under the block is smooth while beneath the spool is rough.
Show that if M=Ir(R−r), no frictional force will act on the spool. Now suppose M=2Ir(R−r), find in which direction will the frictional force act? Also find in this case the rate of increase of length 'ab' of the thread at time t after the application of force. (No slipping occurs.)

For translational motion
F−T−f=mac.m.……(1)
For rotational motion
(Tr+fR)=Iα……(2)
As per given condition if frictional force is zero then,
⇒α=ac.m.R
Hence, Tr+fR=Iac.m.R
⇒T=Iac.m.Rr−f.Rr....(3)
⇒T=Ma'
Since string ab remains tangent, hence acceleration of point a and that of point b is same.
⇒a'=ac.m.R(R−r)
⇒T=Mac.m.R(R−r)......(4)
From Eqs. (3) and (4) , we get
Mac.m.R(R−r)=Iac.m.R(R−r)=Iac.m.R.r−f.Rr.....(5)
Putting f=0 in Eq. (5)
M=Ir(R−r)
Putting the value of M=2Ir(R−r) in Eq.(5), we get
f=−Iac.m.R2.......(6)
Negative sign indicates that friction is acting in the opposite direction of our assumption i.e. in forward direction.
From Eqs. (1), (3) and (6), we get
F−2Iac.m.Rr+Iac.m.R2=mac.m.
⇒ac.m.=F(m+2IRr−IR2)⇒α=FR(m+2IRr+IR2)
∴T=ma'
d2(ab)dt2=α(R−r)−a'=F(R−r)R(m+2IRr−IR2)−2IcmmRr
=F(R−r)R(m+2IRr−IR2)−2ImRrF(m+2IRr−IR2)
=FR(m+2IRr−IR2)[R−r−2Imr]
∴ Rate of increase in length ab=(=vab)=FR(m+2IRr−IR2)[R−r−2Imr]

Topper's Solved these Questions
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View Solution
Knowledge Check
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2A block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
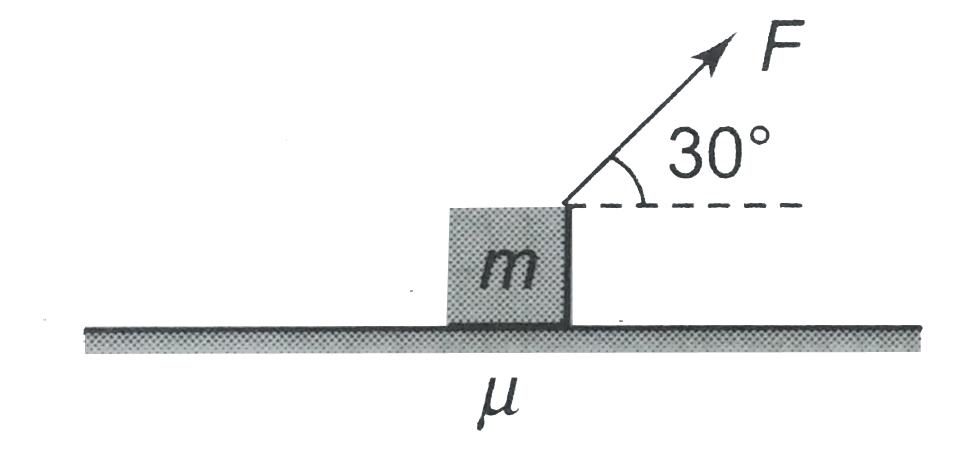 AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)
AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)A block of mass m is placed in contact with one end of a smooth tube of mass M. A horizontal force F acts on the tube in each case (i) and (ii). Then,
 Aam=0andaM=FM in (i)Bam=aM=FM+m in (i)Cam=aM=FM+m in (ii)DForce on m is (mF)/(M+m) in (ii)
Aam=0andaM=FM in (i)Bam=aM=FM+m in (i)Cam=aM=FM+m in (ii)DForce on m is (mF)/(M+m) in (ii)
A wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
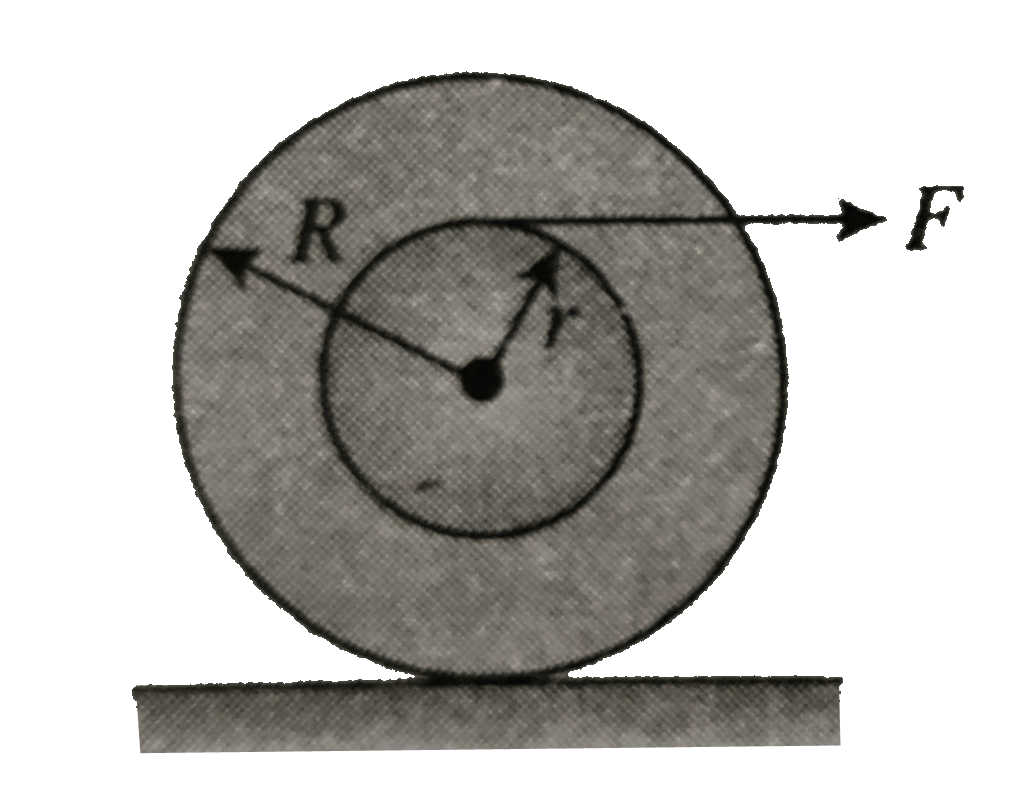
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View SolutionTwo blocks of mass m1andm2 lie on smooth horizontal table in contact with each other as shown in figure
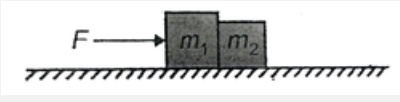
If a force F is applied to the mass m1 then the contact force between the block will be
View SolutionA block of mass m is on the smooth horizontal surface of a plank of mass M The plank is on smooth horizontal surface Now, a constant horizontal force F acts on M. Now, for a person standing on the ground:

View SolutionA block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
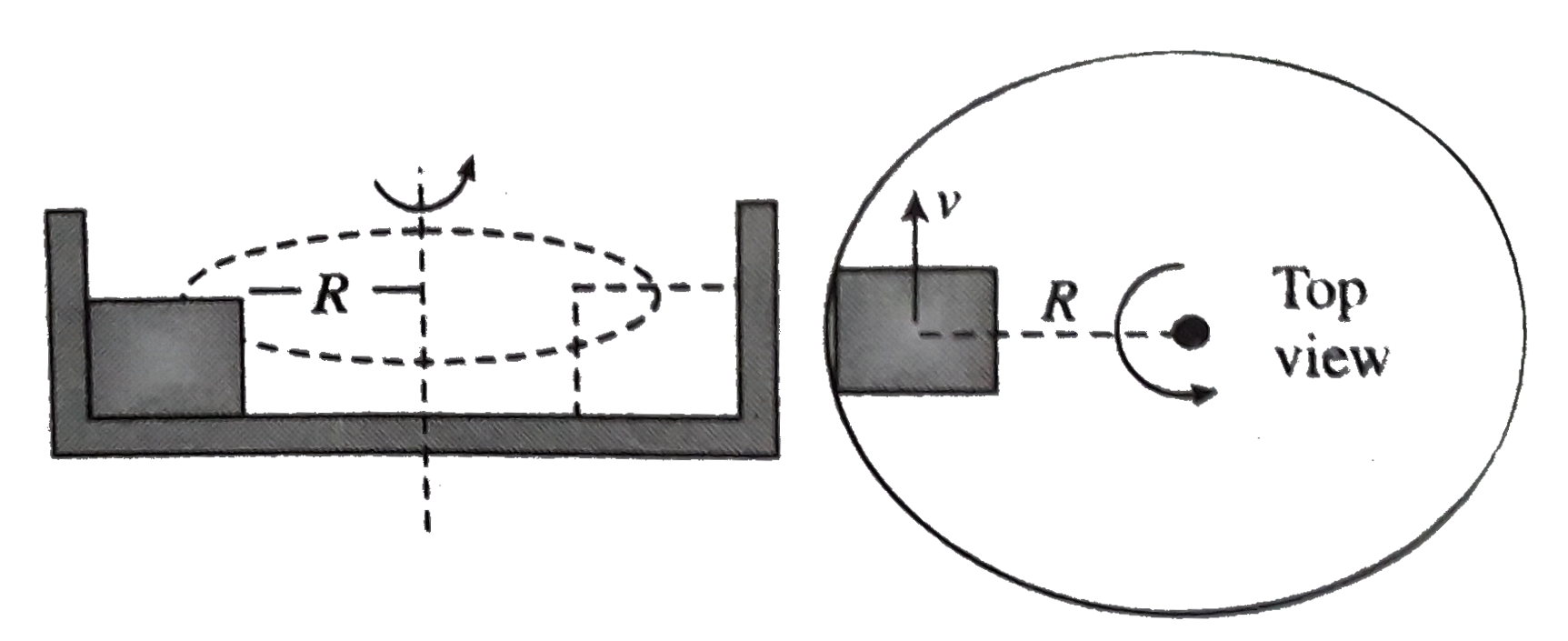
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
View Solution
