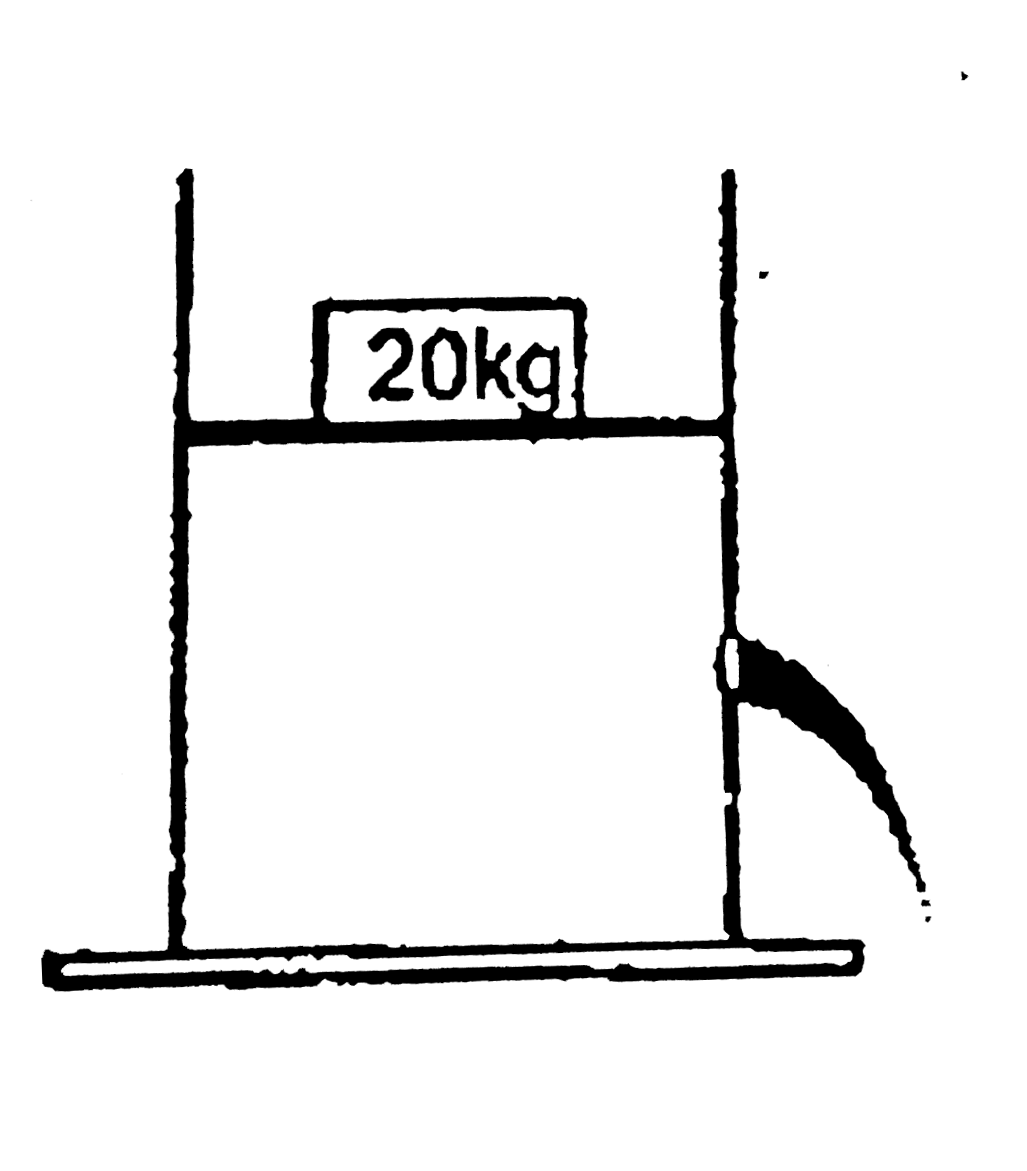
A long cylindrical tank of cross-sectional area $0.5 m^{2}$ is filled with water. It has a small hole at a height $50 c m$ from the bottom. A movable piston of cross-sectional area almost equal to $0.5 m^{2}$ is fitted on the top of the tank such that it can slide in the tank freely. A load of $20 k g$ is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

Video Solution

Text Solution

Verified by Experts

With respect to the opening the height of the piston is $0.5 m$ .
Pressure at the top is $P_{1} = P_{0} + \frac{20 \times 10 N}{0.5 m^{2}}$
where $P_{0}$ is the atmospheric pressure.
Pressure at the opeing is $P_{2} = P_{0}$ , From Bernoulli's equation,
we have
$P_{1} + ρ g h + \frac{1}{2} ρ v_{1}^{2} = P_{2} + \frac{1}{2} ρ v_{2}^{2}$
On solving, we get $v_{2} = 3.3 m / s = v_{x}$ (say)
$v_{y} = \sqrt{2 g h}$
$v = \sqrt{v_{x}^{2} + v_{y}^{2}} = 4.56 m / s$

|

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A cylindrical tank having cross-sectional area A is filled with water to a height of $2.0$ m. A circular hole of corss-section area is opened at a height of 75 cm from the bottom. If $a / A = \sqrt{0.2,}$ then velocity with which waer emerges from the hole is
$(g = 9.8 m s^{- 2})$
A $4.9 m s^{- 1}$
B $4.95 m s^{- 1}$
C $5.0 m s^{- 1}$
D $5.5 m s^{- 1}$
Question 2 - Select One
The inductance of a solenoid $0.5 m$ long of cross-sectional area $20 c m^{2}$ and with $500$ turns is
A $12.5 m H$
B $1.25 m H$
C $15.0 m H$
D $0.12 m H$
Question 3 - Select One
A cyclinderical vessel of cross-sectional area $1000 c m^{2}$ , fitted with a frictonless piston of mass $10 k g$ , and filled with water completely. A small hole of cross-sectional area $10 m m^{2}$ is opened at a point $50 c m$ deep from the lower surface of the piston. The velocity of efflux from the hole will be
A $10.5 m / s$
B $3.4 m / s$
C $0.8 m / s$
D $0.2 m / s$

FIITJEE-FLUID MECHANICS-Example

Home
Ask Doubt
Profile