A solid spherical region having a spherical cavity whose daimeter is equal to the radius of the spherical region, has a total charge . Find the electric field and potential at a point as shown.

Charge density
Using the superposition principle,
Similarly,
Topper's Solved these Questions
Similar Questions
A solid spherical region having a spherical cavity. whose diameter R is equal to the radius of the spherical region, has a total charge Q. The electric field at a point P as shown is Q28πɛ0⎡⎢ ⎢ ⎢⎣Ax2−B(x−R2)2⎤⎥ ⎥ ⎥⎦. Find (A−B).
'(##CEN_KSR_PHY_JEE_C18_E01_029_Q14##)'
View SolutionElectric charge q is uniformly distributed in a spherical space from which a cavity of diameter equal to the radius R of the spherical space has been removed. Calculate the potential and field at a point P lying on the diameter of the cavity at a distance r>r/2 but lt R from the centre of the sphere.
View Solution
Knowledge Check
A solid spherical region, having a spherical cavity whose diameter R is equal to the radius of the spherical region, has a total charge Q. Find the electric field at a point P as shown in figure
 .AQ18πε0⎡⎢ ⎢ ⎢⎣4x2−1(x−R2)2⎤⎥ ⎥ ⎥⎦BQ28πε0⎡⎢ ⎢ ⎢⎣8x2−1(x−R2)2⎤⎥ ⎥ ⎥⎦CQ28πε0[8x2−1(x−R)2]DQ18πε0[4x2−1(x−R)2]
.AQ18πε0⎡⎢ ⎢ ⎢⎣4x2−1(x−R2)2⎤⎥ ⎥ ⎥⎦BQ28πε0⎡⎢ ⎢ ⎢⎣8x2−1(x−R2)2⎤⎥ ⎥ ⎥⎦CQ28πε0[8x2−1(x−R)2]DQ18πε0[4x2−1(x−R)2]A spherical shell of radius R has a charge +q units. The electric field due to the shell at a point
Ainside is zero and varies as r−1 outside itBinside is constant and varies as r−2Cinside is zero and varies as r−2 outside itDinside is constant and varies as r−1 outside itThree conducting spherical shells have charges q,−2q and 3q as shown in figure. Find electric Potential at point P as shown in figure.
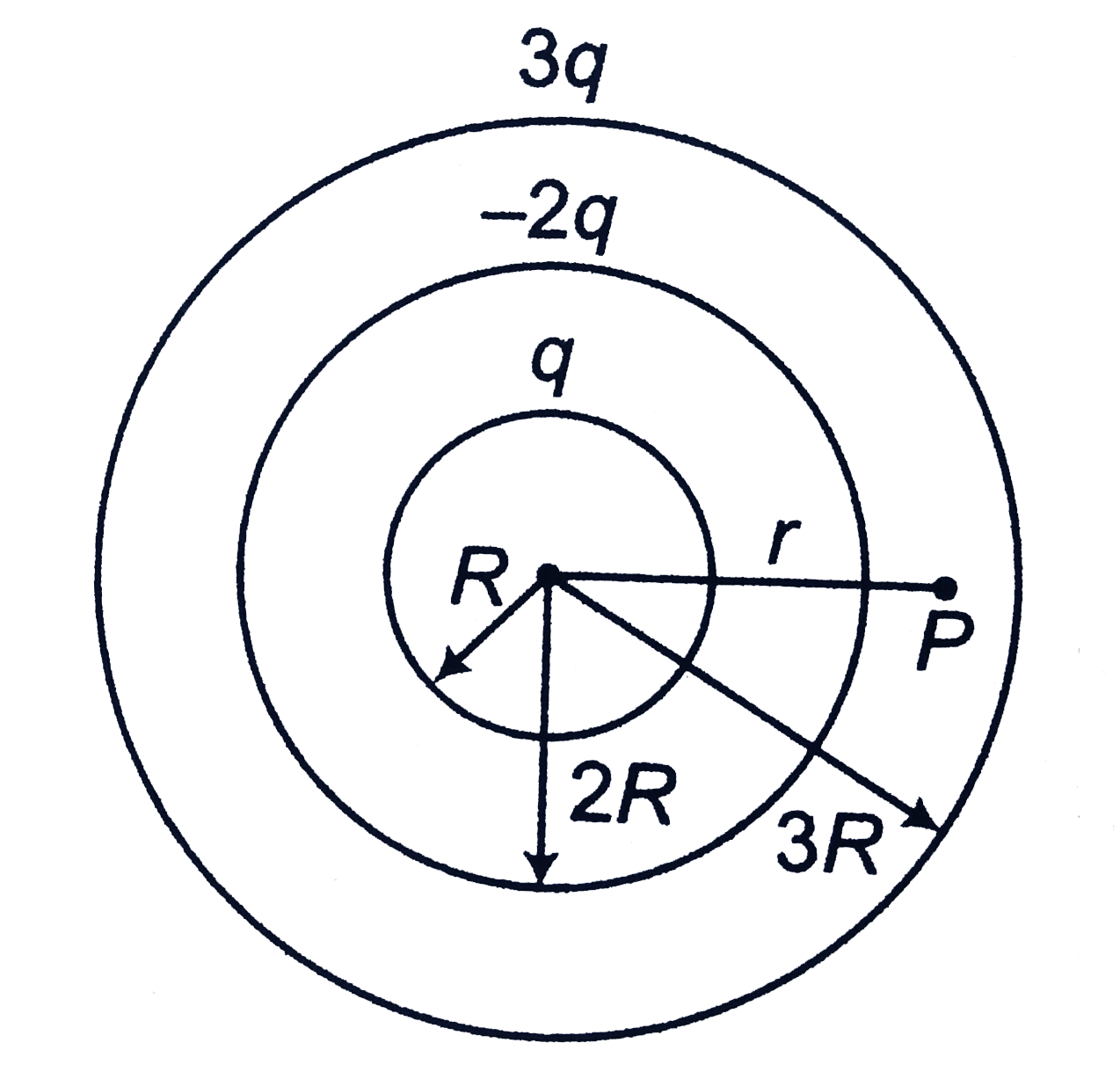 Akq(12r−1r)Bkq(1R−1r)Ckq(12R−1r)Dkqr−k(2q)r+k3qR
Akq(12r−1r)Bkq(1R−1r)Ckq(12R−1r)Dkqr−k(2q)r+k3qR
Here =kq(1R−1r)
Electric Potential Due To A Spherical Shell & Solid Sphere|Relation Between Electric Field And Potential
View SolutionConsider a thick walled metallic spherical shell with inner radius a and outer radius b. No charge is given to the spherical shell. A point charge +Q is kept at the centre. Find the electric potential at a point distance x from the centre where 0<x<∞.
View SolutionA non-conducting sphere of radius R has a spherical cavity of radius R/2 as shown. The solid part of the sphere has a uniform volume charge density ρ. Find the magnitude and direction of electric field at point (a) O and (b) A.

View SolutionA solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnitude) at point 'C' inside the cavity
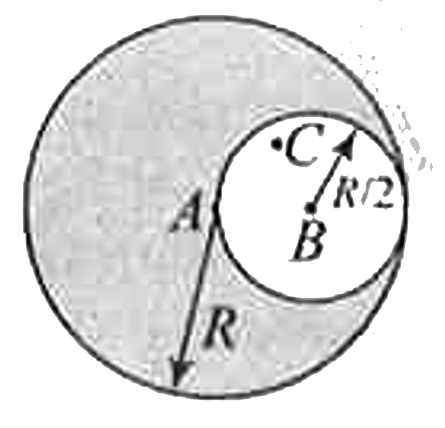
View SolutionA spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
View Solution
