_S01_025_Q01.png)
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kg/m3 and spring constant of the spring =50N/m. Take g=10m/s2
The specific gravity of the block =0.8. Hence the height inside water =3cm×0.8=2.4cm. The height outside water =3cm−2.4=0.6cm. Suppose the maximum weight that can be put without wetting it is W. The block in this case is completely immersed in the water. The volume of the displaced water
= volume of the block =27×10−6m3.
Hence, the force of buoyancy
=(27×10−6m3)×1(1000kg/m3)×(10m/s2)=0.27N.
The spring is compressed by 0.6cm and hence the upward force exerted lby the spring
=100N/m×0.6cm=0.6N.
The force of buoyancy and the spring force taken together balance the weight of the block plus the weight W put on the block. The weight of the blok is
W'=(27×10−6m)×(800kg/m3)×(10m/s2)=0.22N.
Thus, W=0.27N+0.6N−0.22N=0.65N.

Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise18videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - I Section (A)5videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Advanced Level Problems8videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,View Solution
,View SolutionA spring is attached to a wooden cubical block of edge 5cm and placed in a water conatiner as shown in figure. Calculate the maximum weight to be placed on the block so that it is just immersed in water completely. Density of wood =700kg/m3, spring constant of spring =70N/m,g=10m/s2. Assume that initially spring is in its normal length.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
Aa(a2ρg+k)Ba(aρg+2k)Ca(aρg2+2k)Da(a2ρg+k2) - Question 2 - Select One
A log of wood of mass 120 Kg floats in water. The weight that can be put on the raft to make it just sink, should be (density of wood =600Kg/m)
A80KgB50KgC60KgD30Kg - Question 3 - Select One
A cubical block of side 0.5 m floats on water with 30% of its volume under water. What is the maximum weight that can be put on the block without fully submerging it under water?
[Take, density of water =103kg/m3]A87.5 kgB30.1 kgC46.3 kgD65.4 kg
A block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
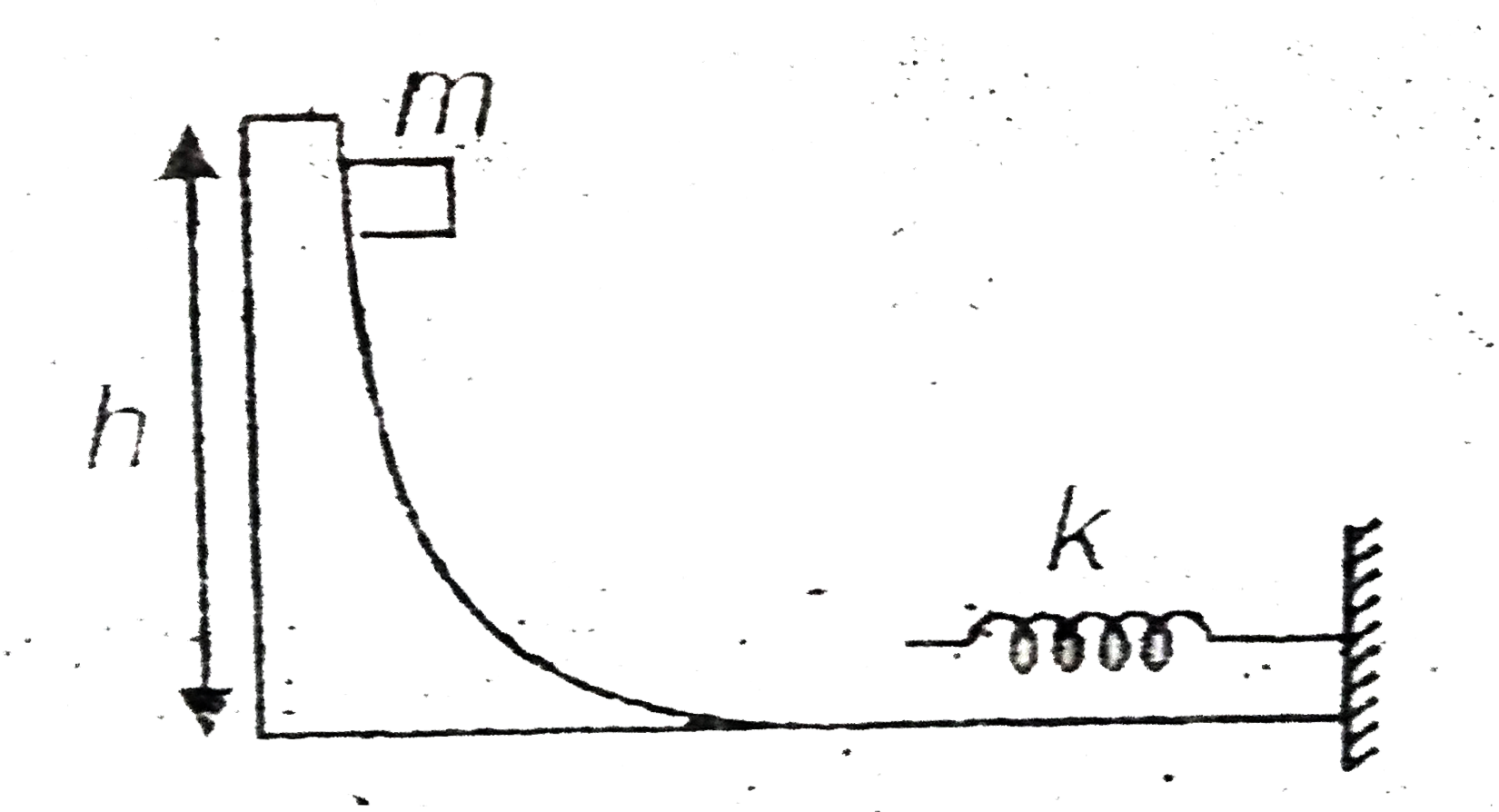 View Solution
View SolutionA cubical block 'A' of mass m0(=a3ρ=3kg) of edge 'a' and density ρ floats in a liquid of density 3ρ. The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a2ρg) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
View SolutionA cubical block of wood of side 5 cm is placed on a table. Find the thrust by the block wood on the table, if density of wood is 5gcm−3 and g is 10 ms−2.
View SolutionA cubical block of wood of length 5 cm is kept on a table top. The density of the block is 800kg/m3 and g=9.8m/s2 . Find the pressure exerted by the wooden block on the table top.
View SolutionA cubical block of wood 10cm on a side, floats at the interface of oil and water as shown in figure. The density of oil is 0.6gcm−3 and density of water is 1gcm−3. The mass of the block is
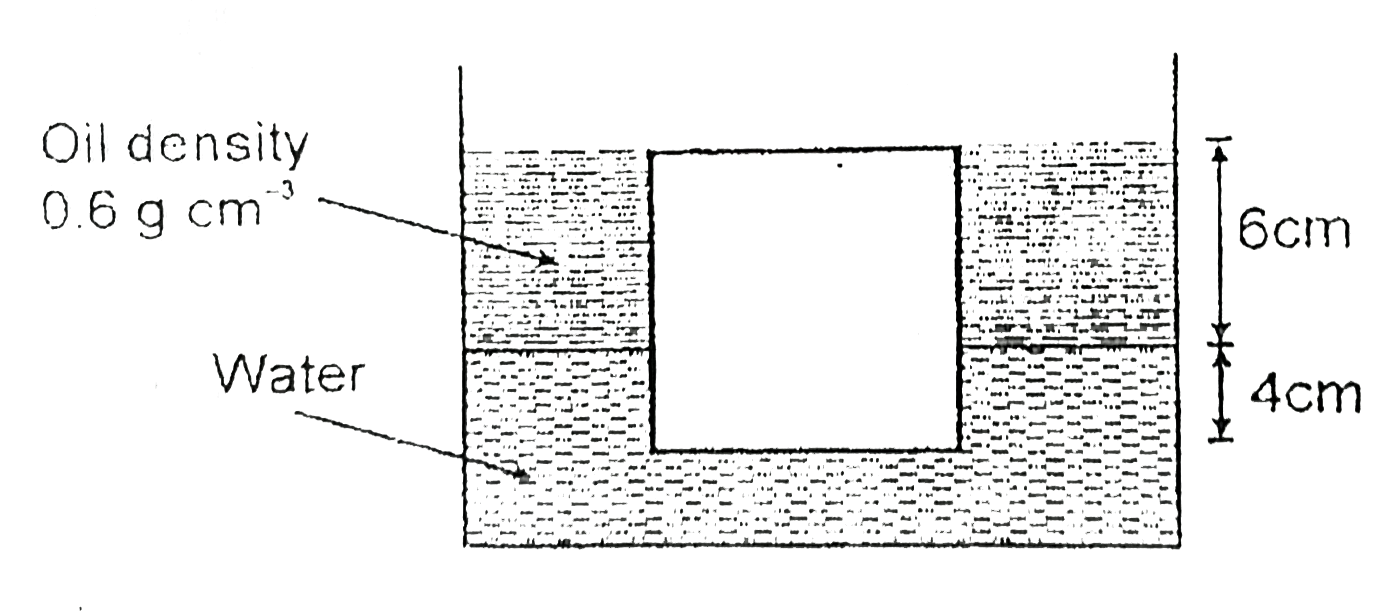 View Solution
View Solution

