A metal piece of mass 10g is suspended by a vertical spring. The spring elongates 10cm over its natural length to keep the piece in equilibrium. A beaker containing water is now placed below the piece so as to immerse the piece completely in water. Find the elongation of the spring. Density of metal =9000kg/m3. Take g=10m/s2.
Let the spring constant be k. When the piece is hanging in air, the equilibrium condition gives
k(10cm)=(0.01kg)(10m/s2)
or k(10cm)=0.1N. ………..(i)
The volume of the metal piece
=0.01kg9000kg/m3=19×10−5m3.
This is also the volume of water displaced when the piece is immersed in water. The force of buoyancy
= weight of the lilquid displace
=19×10−5m3×(1000kg/m3)×(10m/s2)
=0.011N.
If the elongation of the spring is x when the piece is immersed in water, the equilibrium condition of the piece gives,
kx=0.1N−0.011N=0.089N. ..........(ii)
By (i) and (ii),x=0.08910cm=0.0089cm.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise18videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - I Section (A)5videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Advanced Level Problems8videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
A copper piece of mas 10 g is suspended by a vertical spring. The sprig elongates 1 cm over its natural lenngth to keep the piece in equilibrium. A beaker containing water is now placed below the piece so as to immerse the piece completely in water. Find the elongation of the spring. Density of copper =9000 kgm^-3. Takeg=10ms−2
View SolutionA spring elongates by 2 cm when a piece of cobalt of mass 20g is suspended from it. A water conatiner is placed below the pieces in such a way that the piece is immersed completely in water. Calculate the elongation produced in the spring.
Density of cobalt =8700kg/m3,Useg=10ms2.View Solution
Knowledge Check
- Question 1 - Select One
A point mass x = 20 kg, is suspended by a massless spring of constant 2000 N/m. The point mass is released when elongation in the spring is 15 cm. The equation of displacement of particle as function of time is (take, g =10m/s2)
 Ay = 10 sin 10tBY = 10 cos 10tCy=10sin(10t+π6)DNone of these
Ay = 10 sin 10tBY = 10 cos 10tCy=10sin(10t+π6)DNone of these - Question 2 - Select One
A 20N metal block is suspended by a spring balance. A beaker containing some water is placed on a weighing machine which reads 40N. The spring balance is now lowered so that the block gets immersed in the water. The spring balance now reads 16N. The reading of the weighing machine will be.
A36 NB60 NC44 ND56 N - Question 3 - Select One
A piece of gold weighs 10g in air and 9g in water. What is the volume of cavity? (Density of gold =19.3gcm−3)
A0.282 ccB0.482 ccC0.682ccDNone of these
A block of mass 200 g is suspended by a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g=10m/s2.
 View Solution
View SolutionA particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation , the spring becomes upstretched . Find the speed when the spring is stretched by 0.20 cm . (Take , g=π2m/s2)
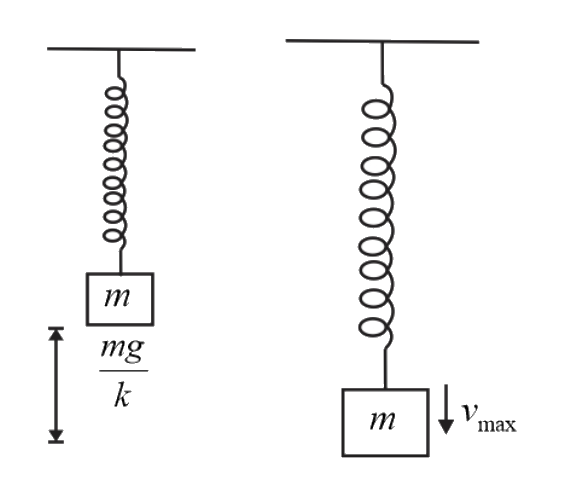 View Solution
View SolutionA point mass m = 20 kg, is suspended by a massless spring of constant 2000 N/M. The point mass is released when elongation in the spring is 15 cm. The equation of displacement of particle as a function of time is ( Take g=10m/s2 )
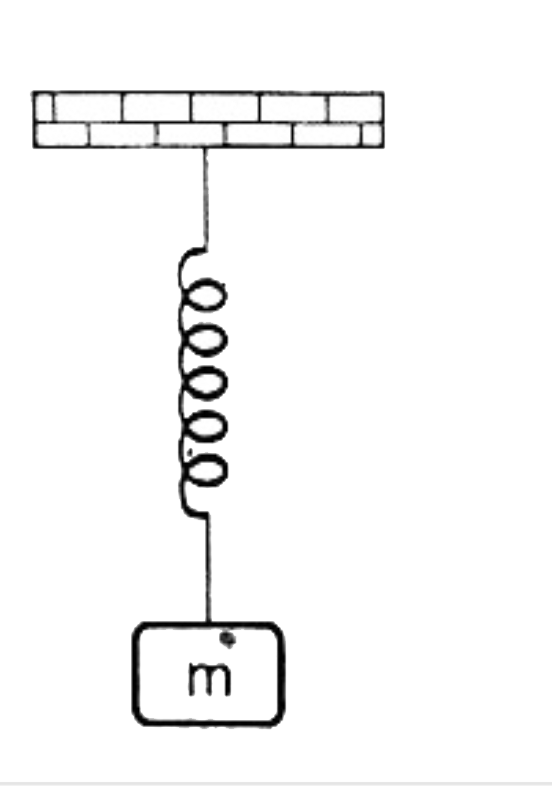 View Solution
View SolutionFrequency of a particle executing SHM is 10Hz. The particle is suspended form a vertical spring. At the highest point of its oscillation the spring is unstretched. Find the maximum speed of the particle: (g=10m/s2)
View SolutionFrom the fixed pulley, masses 2 kg, 1 kg and 3 kg are suspended as shown is figure. Find the extension in the spring when acceleration of 3 kg and 1 kg is same if spring constant of the spring k = 100 N/m. (Take g=10ms−2)
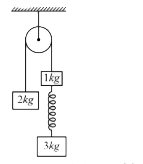 View Solution
View Solution

