A cylinder of 150 mm radius rotates concentrically inside a fixed cyli

A solid cylinder of radius 0.5 m and mass 50 kg is rotating at 300 rpm. Then the torque which will bring it to rest in 5 seconds is
A $25 π N m$
B $\frac{25 π}{2} N m$
C $50 π N m$
D $100 π N m$
A small sphere of mass $m$ and radius $r$ is placed inside a horizontal hollow cylinder of radius $R$ . Now cylinder rotating with some angular acceleration which slowly increases from zero to certain value $α$ .

AMaximum angle $θ$ formed by line joining centre will be $θ = {sin}^{- 1} (\frac{2 α R}{5 g})$
BAngular velocity of sphere will be $ω^{'} = \frac{ω r}{R}$ where $ω$ is angular velocity of cylinder
CSphere will keep rotating at lowest position
DK.E. of sphere becomes constant when it reaches maximum height
The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed $v_{1}$ . It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I

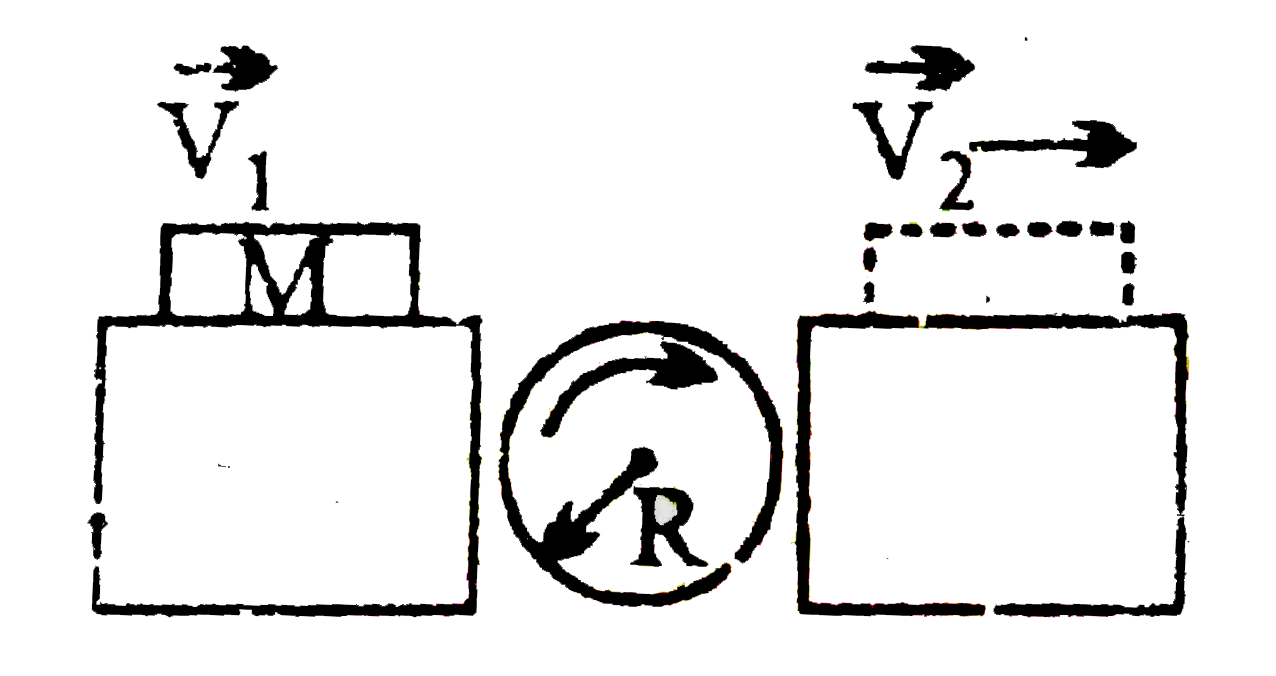
If $ω$ is final angular velocity of the cylinder, then
A $v_{1} = ω R$
B $v_{2} = ω R$
C $v_{1} < ω R$
Dnone

The correct Answer is: $η = 0.77 N - sec / m^{2}$