Two interacting particles form a closed system whose centre of mass is at rest. Fig. illustrates the positions of both particles at a certain moment and the trajectory of the particle of mass $m_{1}$ . Select the trajectory of the particle of mass $m_{2}$ if $m_{2} = m_{1}$ .

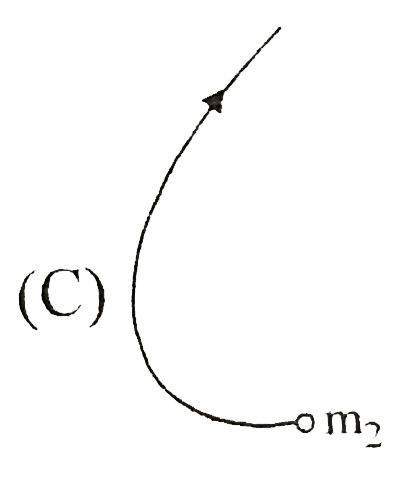
ocr_image

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

A particle $(A)$ of mass $m_{1}$ elastically collides with another stationary particle $(B)$ of mass $m_{2}$ . Then :
A $\frac{m_{1}}{m_{2}} = \frac{1}{2}$ and the particles fly a part in the opposite direction with equal velocities.
B $\frac{m_{1}}{m_{2}} = \frac{1}{3}$ and the particles fly apart in the opposite direction with equal velocities.
C $\frac{m_{1}}{m_{2}} = \frac{2}{1}$ and the collision angle between the particles is $60^{\circ}$ symmetrically.
D $\frac{m_{1}}{m_{2}} = \frac{2}{1}$ and the particles fly apart symmetrically at an angle $90^{\circ}$
The position of centre of mass of a system consisting of two particles of masses $m_{1}$ and $m_{2}$ seperated by a distance L apart , from $m_{1}$ will be :
A $\frac{m_{1} L}{m_{1} + m_{2}}$
B $\frac{m_{2} L}{m_{2} + m_{2}}$
C $\frac{m_{2}}{m_{1}} L$
D $\frac{L}{2}$
If ${\to R}_{C M}$ is the position of the centre of mass of a system of two particles of masses $m_{1}$ and $m_{2}$ then ${\to R}_{C M}$ is given by :
A $\frac{m_{1} + m_{2}}{m_{1} {\to r}_{1} + m_{2} {\to r}_{2}}$
B $\frac{m_{1} m_{2}}{m_{1} {\to r}_{1} + m_{2} {\to r}_{2}}$
C $\frac{m_{1} {\to r}_{1} + m_{2} {\to r}_{2}}{m_{1} + m_{2}}$
D $\frac{m_{1} {\to r}_{1} + m_{2} {\to r}_{2}}{m_{1} m_{2}}$